1. Из условия задачи - курицы у нас все разные. То есть если у нас мы возьмем какой-то набор птиц, в котором есть курица; и заменим эту курицу на другую, то получится другой набор
В таком понимании задачи, всего различных комбинаций птиц - 512 (учитывая комбинацию без птиц вовсе, каждую птицу можно взять или не взять, птиц всего 9, 2^9 вариантов). Воспользуемся кругами Эйлера к этой задаче: пусть круги означают кол-во комбинаций БЕЗ указанных птиц
БЕЗ гусей у нас 2^7 = 128 вариантов
БЕЗ кур - 64, а БЕЗ уток - 32 варианта
Далее, найдем кол-во комбинаций без гусей и без уток, без гусей и без кур, без кур и без уток. Без всех птиц у нас 1 единственная комбинация. Используя это, найдем кол-во вариантов для каждого из подмножества. Далее, вычтем из 512 все эти подмножества. Получим количество вариантов, где точно есть и утки, и гуси, и куры
ответ: 315
1.
Выносим общее из скобок
А) 4х²-12х = 4х(х-3)
Группируем (можно по-разному)
Б) 2а + 4b – ab – 2b² = 4b– 2b² + 2а – ab = 2b(2-b) + a(2-b) = (2b + a)(2-b)
Это формула сокращенного умножения
В) 9х² – 16 = (3х - 4)(3х+4)
Г)х³ – 8х² + 16х 2. Не поняла, почему тут пропуск, тут 16х²?
2.
(х – 4)² – 49 = 0
х² - 8х + 16 - 49 = 0
х² - 8х - 33 = 0
D = b² - 4ac = 64 - 4 × (-33) = 64 + 132 = 196 = 14²
x 1,2 =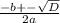 =
= 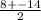 =
=