Предположим, что х часов - это время работы первой бригады, тогда (х+4) часа - время работы второй бригады, примем всю работу за 1
согласно этим данным составим и решим уравнение для совместной работы:
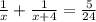 /·24x(x+4)
/·24x(x+4)
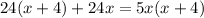
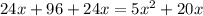
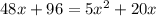
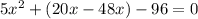
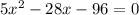
Cчитаем дискриминант:
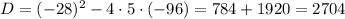
Дискриминант положительный
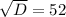
Уравнение имеет два различных корня:
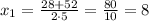
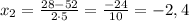
не удовлетворяет условию задачи, так как отрицательное время быть не может
х=8 (ч) - I бригада.
х+4=8+4=12 (ч) - II бригада.
Следовательно, первая бригада заасфальтирует участок дороги за 8 часов, а вторая за 12 часов.
ну да хорошо готовое решение взять и списать и потом где нарушения я же доказал что просто домножены обе части на 3
1)1см к20км тоесть 1 см на карте это 20км в живую
80/4=х/1 х=(80*1)/4 х=20
2)нет (так как это пропорция просто домножана на 3 как левая так и правая часть)
5:8,2=15:24,8
5 и 8,2 (домножаем на 3) 15/24,6 не равно 15 /24,8
3)перекрестное правело х=(9*8)/5 х=14,4
4)аналогично х=(7*12)/3 х=28 (на самом деле дробь сделай плочкой и там вид будет легче это ко все заданиям применяй)
5)аналогично 10/20=х/40 х=(10*40)/25 х=16
6)аналогично 60/3=2,5/х х=(60*3)/2,5 х=72
7)аналогично 12/15=20/х х=(15*20)/12 х=25
/-это знак деления если что то непонятно пиши в личку и поставь самый лучшее решение мне балы надо тоже что бы мне сделали домашку)))
1(2x-1)(4x2-2x+1)-4x(2x2-1)=5x-2
раскроем скобки
8x3-4x2+2x-4x2+2x-1-8x3+4x = 5x-2
-8x2+3x+1 = 0
8x2-3x-1 = 0
Вычислим дискриминант D
D = b2 - 4ac = ( – 3)2 – 4·8·( – 1) = 41
x1 = -b + √ D = 3 + √ 41 = 3 + √ 41
2a 2·8 16
x2 = -b – √ D = 3 – √ 41 = 3 – √ 41
2a 2·8 16