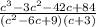
Объяснение:
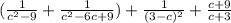
Это задание в первую очередь ориентировано на проверку ваших знаний ФСУ или Формул Сокращённого Умножения.
Давайте просканируем пример на их наличие.
1.
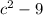- Это разность квадратов, а именно квадрата числа с и числа 3. Возможно вы зададите резонный вопрос - а зачем нам это отслеживать. В работе с дробями важно уметь находить взаимосвязи между знаменателями. 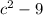раскладывается рак (с-3)(с+3)
2. 
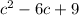- знаменатель второй дроби и является квадратом разности(смотрим по знаку перед вторым числом). Он раскладывается как (с-3)(с-3).
Что-то напоминает не так ли? Таким образом, с-3 это общий множитель обоих знаменателей. Значит нужно перемножит каждую дробь на оставшийся общий множитель другой дроби
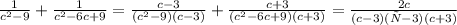
Я специально оставила дробь полностью раскрытой, т.к. она нам ещё может понадобиться.
3.
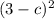- аналогично пункту 2 квадрат разности. Раскладывается практически аналогично. Но т.к. от перемены мест слагаемых сумма не меняется это исправимо.
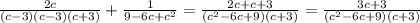
Дальше приведём получившуюся дробь и оставшуюся к общему знаменателю.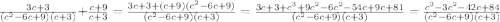
используем теорему виетта: x^2+px+q=0. x1+x2=-p; x1*x2=q. x1+x2=3/5+3/5=6/5; x1*x2= 3/5*3/5=9/25. подставляем: x^2-6/5x+9/25=0. X^2-1,2x+0,36=0.