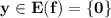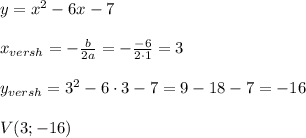
Функция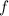 
называется парной, если:
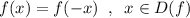
Учитывая это попробуем узнать, могут ли выполняться равенства:
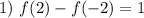
Поскольку по условию функция 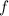парная, то:
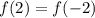
Любое число минус это же число = 0. Значит равенство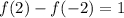 
выполняться не может. Можно это доказать. Пусть 
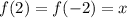, тогда:
- не верно. Следовательно, уравнение не имеет корней и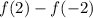 
не может быть равно единице.
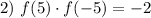
Поскольку по условию функция 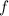парная, то:
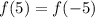
При умножении двух равных чисел не может получиться отрицательное число. Потому что при умножении положительных чисел получается положительное число, и при умножении отрицательных чисел также получается положительное число. То есть:
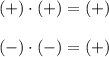
Значит равенство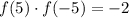 
выполняться не может (поскольку -2 -- отрицательное число). Это можно доказать. Пусть 
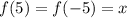, тогда 
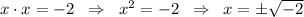корня квадратного из отрицательного числа не существует. Следовательно уравнение не имеет решений и 
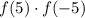не может быть равно -2.
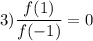
Поскольку по условию функция 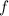парная, то:
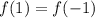
При делении равных чисел результат всегда равен 1. Значит равенство 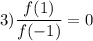выполняться не может. Доказательство:
Пусть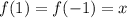 
, тогда 
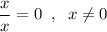. Домножим обе части уравнения на x, тогда 
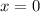, что не удовлетворяет ОДЗ. Значит уравнение не имеет корней и 
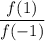не может быть равно 0.
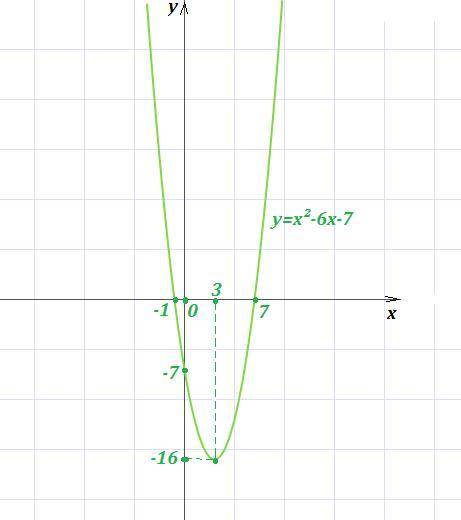
Решение.
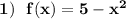
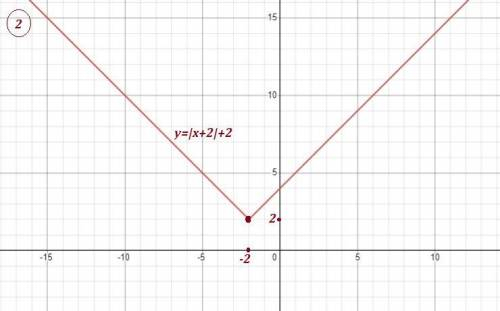
Это квадратичная функция , ограничений на переменную х не накладываются , поэтому
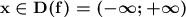- область определения функции .
Графиком квадратичной функции является парабола, причём, т.к. коэффициент перед х² равен -1<0 , то ветви параболы направлены вниз , и выше вершины в точке (0;5) графика существовать не будет . Поэтому самое максимальное значение , которое принимает заданная функция равно f(x)=5 . Поэтому область значений функции
![\boldsymbol{y\in E(f)=(-\infty ;\ 5\ ]}](/tpl/images/4978/1730/fd3a0.png)
Cмотри рисунок .
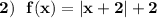
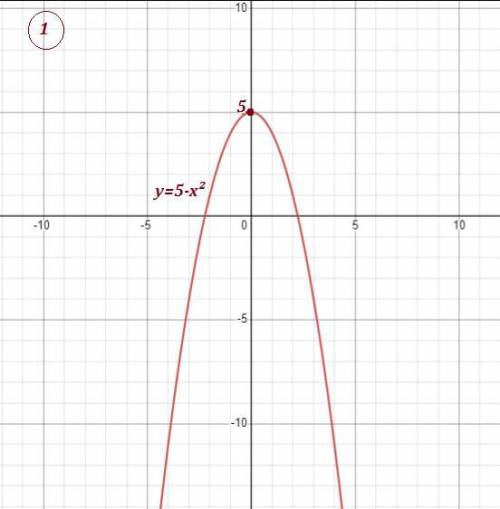
Графиком этой функции является график функции у=|x| ( угол , ветви вверх ) сдвинутый вдоль оси ОХ на 2 единицы влево и вдоль оси ОУ на 2 единицы вверх .
ООФ: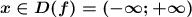 
ОЗФ: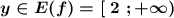 
Смотри рисунок .
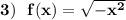
Под знаком квадратного корня может быть записано только неотрицательное выражение.
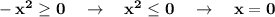
ООФ: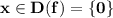 
- это множество из одного элемента .
ОЗФ: 
