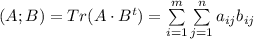
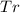- след матрицы, то есть сумма диагональных элементов, 
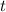- знак транспонирования. Соответственно квадрат длины вектора (то есть матрицы A) равен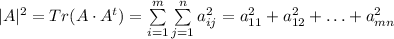 
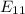, у которой в пересечении первой строчки и первого столбца стоит единица, а остальные нули, потом матрицы 
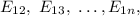далее переходим на вторую строчку и так далее до последней матрицы 
.
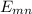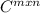скалярное произведение задается по той же формуле, только у второй матрицы элементы нужно заменить на комплексно сопряженные:
.
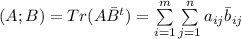Стоимость доставки М = х + п*у, где х - стоимость доставки к дому,
у - стоимость доставки на 1 этаж,
п - количество этажей
Тогда: М₄ = 890 = х + 4у
М₇ = 980 = х + 7у решаем систему
х = 980 - 7у - подставляем в 1-е уравнение:
980 - 7у + 4 у = 890
90 = 3у
у = 30 тогда х = 980 - у = 980 - 210 = 770
и М₁₁ = 770 + 11*30 = 1100 (руб)