Во-первых, отметим, что аргументы логарифмов должны быть строго больше нуля, но поскольку аргументы -- целые числа, то они должны быть хотя бы 
. С другой стороны, как нетрудно заметить, их сумма равна 
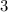. Стало быть, каждый из них равен единице: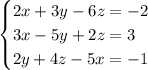 
Детерминант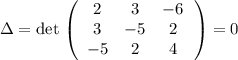 
(-(1 строка) - (2 строка) = (3 строка)). Решение можно параметризовать: 
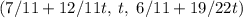, откуда 
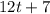должно делиться на 
, а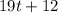 
должно делиться на 
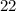. Тогда 
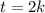, потому 
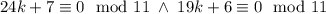. Из первого 
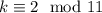, а из второго -- 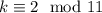. Итак, 
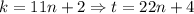, поэтому решение переписывается в виде 
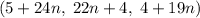. Итак, слева у исходного неравенства стоит нуль, а справа -- 
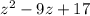. Получаем, что 
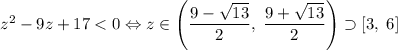, а потому подходит только 
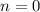и соответствующая тройка 
.
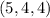В решении.
Объяснение:
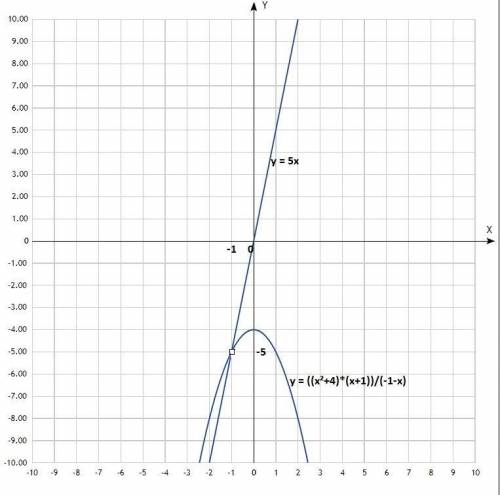
1) Постройте график функции у = ((x²+4)*(x+1))/(-1-x).
Преобразовать уравнение для упрощения:
((x² + 4)*(x + 1))/(-1 - x) = ((x² + 4)*(x + 1))/ -(1 + x) =
Сократить числитель и знаменатель на (х + 1);
= (х² + 4)/ (-1) = -х² - 4;
у = -х² - 4;
Уравнение квадратичной функции, график - парабола со смещённым центром, ветви направлены вниз.
ОДЗ: х ≠ -1 (при этом значении х знаменатель дроби равен нулю, функция не определена).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -2 -1 0 1 2
у -8 -5 -4 -5 -8
Следует иметь ввиду, что график хоть и строится по вычисленным точкам, точка с координатами (-1; -5) является "выколотой", функция в этой точке не существует.
2) Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Прямая y = kx имеет с графиком ровно одну общую точку, если проходит через указанную "выколотую" точку.
Найти уравнение этой прямой.
Вычислить значение k. Для этого в уравнение подставить известные значения х и у (координаты "выколотой" точки):
y = kx
-5 = k * (-1)
-5 = -k
k = 5;
Уравнение прямой:
у = 5х;
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. График - прямая линия, проходящая через начало координат.
Таблица:
х -1 0 1
у -5 0 5
При k = 5 прямая y = kx имеет с графиком ровно одну общую точку.
а)
x1 = -11
x2 = 11
б)
c1 = -6
c2 = 6