Объяснение:Построение графика любой функции необходимо начинать с анализа уравнения этой функции.
В уравнении функции первое слагаемое 2/х , функция у=2/х- обратно-пропорциональная, вида y=k/x? k>0; её график -гипербола в 1 и 3 четверти; существует при любом значении х, кроме нуля, т.е. х≠0. Чем больше точек для её построения зададите, тем лучше, точнее будет. Но лучше не менее пяти точек для одной ветви гиперболы.
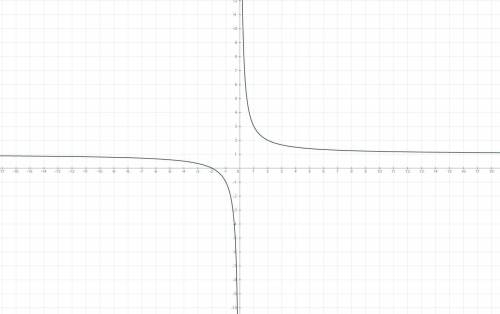
Замечание: ветви гиперболы не пересекают прямую у=1, т.е. график функции у=2/х поднят вверх вдоль по оси у на 1)
Как искать точки?
Для этого подставим в уравнение функции числовое значение х вместо х и вычислим у:
если х=0,5 то у= 2/0,5+1= 4+1=5
если х=1 то у=2/1+1= 2+1= 3
если х= 2 то у= 2/2 +1= 1+1=2
если х= 4, то у= 2/4+1= 0,5+1=1,5
если х=8, то у=2/8+1= 0,25+1=1,25
Аналогично отрицательные значения х:
если х=-0,5 то у=2/(-0,5) +1 =-3
если х=-1 то у=2/(-1)+1= -2+1= -1
если х= -2 то у= 2/(-2 )+1= -1+1=0
если х= -4, то у= 2/(-4)+1= -0,5+1=0,5
если х=-8, то у=2/(-8)+1= - 0,25+1=0,75
Значения этих точек лучше записать для удобства в таблицу:
х 0,5 1 2 4 8 -0,5 -1 -2 -4 -8
у 5 3 2 1,5 1,25 -3 -1 0 0,5 0,75
Отметить на координатной плоскости и соединить каждую ветвь гиперболы плавной линией.
a) Выражение имеет смысл когда подкоренное выражение неотрицательно. Тогда
-x ≥ 0 ⇔ x ≤ 0 ⇔ x∈(-∞; 0].
b) В силу пункта а) область определения функции : D(y)=(-∞; 0].
Значение квадратного корня неотрицательно, поэтому множество значений функции : E(y)=[0; +∞).
Чтобы построить график функции определим несколько значений функции:
График функции в приложенном рисунке 1.
c) Чтобы показать на графике значения х при у=2 и y=2,5 сначала определим эти значения. Для этого решаем уравнения:
Получили целое число.
Приближенные значение х=–6,25≈–6.
Значения х показаны на приложенном рисунке 2.
Объяснение:a) Выражение имеет смысл когда подкоренное выражение неотрицательно. Тогда
-x ≥ 0 ⇔ x ≤ 0 ⇔ x∈(-∞; 0].
b) В силу пункта а) область определения функции : D(y)=(-∞; 0].
Значение квадратного корня неотрицательно, поэтому множество значений функции : E(y)=[0; +∞).
Чтобы построить график функции определим несколько значений функции:
График функции в приложенном рисунке 1.
c) Чтобы показать на графике значения х при у=2 и y=2,5 сначала определим эти значения. Для этого решаем уравнения:
Получили целое число.
Приближенные значение х=–6,25≈–6.
Значения х показаны на приложенном рисунке 2.