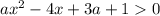
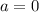 квадратное неравенство вырождается в линейное
квадратное неравенство вырождается в линейное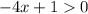
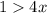
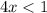
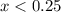
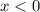
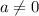

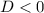 ) - отлично, график параболы выше оси Ох - неравенство выполняется
) - отлично, график параболы выше оси Ох - неравенство выполняется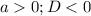
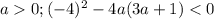

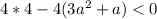
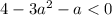
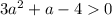
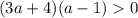
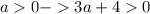 авмтоматически
авмтоматически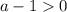 или
или 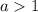
 -
- 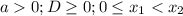 ;
; 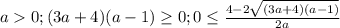
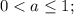 - с первых двух неравенств (аналогично по рассуждениям относительно первого случая)
- с первых двух неравенств (аналогично по рассуждениям относительно первого случая)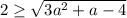
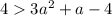
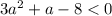 - что очевидно верно при условиях
- что очевидно верно при условиях 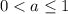
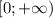
1) Возьмем производную, приравняем ее к 0, чтобы найти точки экстремума:
y'>0 при любых х, значит функция возрастает => большему значению х соответствует большее значение у (и наоборот).
Значит, наименьшее значение функция примет в нижнем пределе, а именно:
2) Рассуждения аналогичны первой задаче
y'<0 при любых х, значит функция убывает => меньшему значению х соответствует большее значение у (и наоборот).
Значит, наибольшее значение функция пример в нижнем пределе, а именно: