Пусть n = x, мне просто так удобнее)
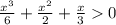
Обе части уравнение умножим на 6:
х³+3х²+2х>0
х(х²+3х+2)>0
х(х+1)(х+2)>0
При любых натуральных значениях х, х(х+1)(х+2) > 0(то есть является натуральным числом)
___________________
2 решение :
Рассмотрим по отдельности каждое слагаемое:
х³/6 > 0 | *6
х³>0
х > 0
То есть х³/6 больше нуля при всех натуральных числах.
____________________________
Если рассмотреть остальные 2 слагаемых, то там будет тоже самое(мне просто лень писать).
____________________________
Если каждое из слагаемых больше нуля, то и сама сумма больше нуля, то есть является натуральным числом)
ответ: в)
Объяснение: квадратичная функция, график-парабола, ветви вверх... условие существования двух различных корней: D>0
(для этой функции дискриминант всегда положителен: (5k^2-6k-11)^2+28k^4>0 для любых k...)
корни будут противоположными числами (т.е. равными по модулю и отличающимися только знаком: 5 и -5; или 1.5 и -1.5), если вершина параболы лежит на оси ОУ, т.е. имеет координаты (0; у) и у<0
при х=0, получим у = -k^4 <0
абсцисса вершины вычисляется по формуле:
-b/(2a) = -(5k^2-6k-11)/14 = 0
5k^2-6k-11=0
D=36+220=16^2
k=(6-16)/10=-1 или k=(6+16)/10=2.6
при этих значениях k вершина будет лежать на оси ОУ
2.6-1=1.6
ответ на приложенной фотографии