Скорость первого катера:
v₁ = 60/t
Скорость второго катера:
v₂ = 60/(t+1)
Скорость сближения катеров:
v = v₁+v₂ = 60/t + 60/(t+1) =
= 60(t+1)+60t)/(t(t+1)) = (120t+60)/(t²+t)
По условию: v = S/t' = 50:1 = 50 (км/ч)
Тогда:
120t + 60 = 50t² + 50t
50t² - 70t - 60 = 0
5t² - 7t - 6 = 0 D = b²-4ac = 49+120 = 169
t₁ = (-b+√D)/2a = 2 (ч)
t₂ = (-b-√D)/2a = -0,6 (ч) - не удовлетворяет условию
Тогда скорость первого катера:
v₁ = 60/t = 60:2 = 30 (км/ч)
Скорость второго катера:
v₂ = 60/(t+1) = 60:3 = 20 (км/ч)
ответ: 30 км/ч; 20 км/ч.
Объяснение:
Пусть х км в час -скорость велосипЕдиста
y км в час - скорость мотоциклиста
встретились через 6 часов, значит велосипЕдист проехал 6х км,
мотоциклист проехал 6у км, а вместе они проехали 240 км
Первое уравнение:
6x+6y=240
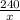 час потратил на весь путь велосипЕдист
час потратил на весь путь велосипЕдист
 час потратил на весь путь мотоциклист
час потратил на весь путь мотоциклист
велосипЕдист потратил на 5 часов больше чем мотоциклист
Второе уравнение
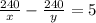
Решаем систему уравнений:
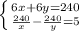



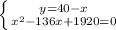

 138 не удовл смыслу задачи
138 не удовл смыслу задачи

О т в е т.
18 км в час -скорость велосипЕдиста
22 км в час - скорость мотоциклиста
n-й член арифметической прогрессии an = a1 +d(n-1)
поэтому а4 = а1 + 3d; а6 = а1 + 5d; а7 = а1 + 6d; а2 = а1 + d; а5 = а1 + 4d;
а4 + а6 - а7 = а1 + 3d + а1 + 5d - а1 - 6d = 11
а1 + 2d= 11 (1)
а2 + а5 = а1 + d + а1 + 4d = 2а1 + 5d
2а1 + 5d = 25 (2)
Из уравнения (1) получим а1 = 11 - 2d (4)
и подставим (4) в уравнение (2)
2 (11 - 2d) +5d = 25
22 - 4d +5d = 25
d = 3
Из уравнения (4) а1 = 11 - 3 = 8
ответ: а1 = 8; d = 3