равные элементы с обоих сторон можно сократить: здесь и в левой, и в правой частях уравнения есть -4х, значит можно сократить этот одночлен. Получится следующее:
опять сократим одинаковые элементы. Здесь это .
1=4,5.
Так как 1 не может ни при каких условиях равняться 4,5; то уравнение не имеет решений.
Распишем формулу, с которой можно рассчитать квадрат расстояния от точки (2; 0,5) до точки с координатами (х; х^2). Почему квадрат? Просто чтобы не париться каждый раз писать значок квадратного корня и не усложнять потом нахождение производной - ведь функция х^2 возрастает на положительном участке числовой оси, т.е. если квадрат расстояния будет минимальным, то и само расстояние тоже будет минимальным. Итак, расписываем, чему равен квадрат расстояния: Найдем производную, приравняем ее к нулю и решим получившееся уравнение, тем самым определим критическую точку (или критические точки): Уравнение производной имеет только один корень, т.е. у функции есть лишь одна критическая точка. Исследуем промежутки монотонности: при х<1 f'(x)<0, функция убывает; при х>1 f'(x)>0, функция возрастает; это означает, что в точке х=1 находится минимум функции. Итак, мы нашли точку параболы у=х^2, расстояние от которой до заданной точки минимально. Это точка с координатами х=1; у=1.
Пусть х га - площадь, которую тракторист планировал вспахивать за день. Тогда х + 6 га - площадь, которую вспахивал тракторист в действительности. По условию задачи, площадь поля = 224 га, следовательно, по плану тракторист должен был завершить работу за 224 : х дней; в условии задачи также указано, что работа была завершена на 12 дней раньше срока. Составим уравнение:
(см. приложенное фото)
Решив уравнение, находим, что тракторист планировал вспахивать по 8 га в день. Теперь определим, за сколько дней тракторист вспахал поле в действительности:
равные элементы с обоих сторон можно сократить: здесь и в левой, и в правой частях уравнения есть -4х, значит можно сократить этот одночлен. Получится следующее:
опять сократим одинаковые элементы. Здесь это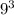 .
.
1=4,5.
Так как 1 не может ни при каких условиях равняться 4,5; то уравнение не имеет решений.
ответ: уравнение не имеет решений.