10000
Объяснение:
Это выражение можно представить как квадрат суммы:
(62+38)^2
62+38=100
Дальше очень просто:
100*100=10000
Более подробно:
62^2+2*62*38+38^2
Пользуясь формулой (a+b)^2=a^2+2ab+b^2
Мы можем понять что 62 это "a" 38 это "b"
Ну а дальше то что в объяснение↑
Удачи)
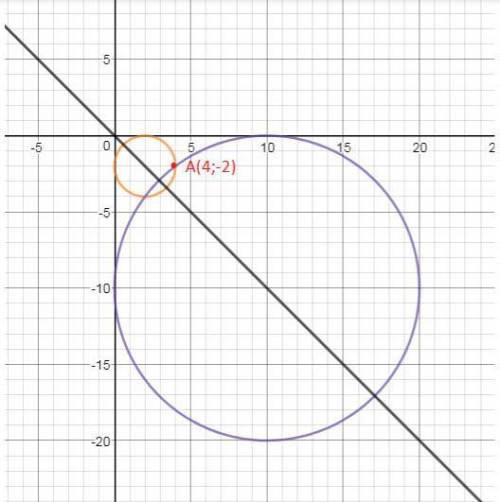
Окружность касается осей координат и проходит через точку, расположенную в четвертой координатной четверти, значит центр окружности лежит на биссектрисе второго и четвертого координатных углов, т.е на прямой y = – x.
и потому центр окружности имеет координаты (R;–R)
Следовательно, уравнение окружности имеет вид
(x – R)2 + (y –(– R))2 = R2.
Поскольку точка A(4;–2) лежит на окружности, координаты этой точки удовлетворяют полученному уравнению,
т.е.
(4 – R)2 + (–2 + R)2 = R2.
16–8R+R2+4–4R+R2=R2
R2–12R + 20 = 0
D = 144–80 = 64
R = 2 или R = 10
(x - 2) 2 + (y + 2) 2 = 4 или
(x - 10) 2 + (y + 10) 2 = 100
.
Объяснение:
Объяснение:
1)Найти координаты точек пересечения прямых с осями координат
а)x−y = −1 преобразуем выражение в уравнение функции:
-у= -1-х
у=1+х
График пересекает ось Ох при у=0.
у=0
0=1+х
-х=1
х= -1
Координаты точки пересечения графиком оси Ох (-1; 0)
График пересекает ось Оу при х=0.
х=0
у=1+х
у=1+0
у=1
Координаты точки пересечения графиком оси Оу (0; 1)
б)2x + y = 4 преобразуем выражение в уравнение функции:
у=4-2х
График пересекает ось Ох при у=0.
у=0
0=4-2х
2х=4
х= 2
Координаты точки пересечения графиком оси Ох (2; 0)
График пересекает ось Оу при х=0.
х=0
у=4-2х
у=4-0
у=4
Координаты точки пересечения графиком оси Оу (0; 4)
2)Найти точку пересечения этих прямых друг с другом.
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
у=1+х у=4-2х
Таблицы:
х -1 0 1 х -1 0 1
у 0 1 2 у 6 4 2
Согласно графика, координаты точки пересечения (1; 2)
(Значения таблиц подтверждают это).
10 000
Объяснение:
(62 + 38 ) ² = 10 000