Вот вместе с проверкой
С применением степени
(квадрат и куб) и дроби
Квадратный корень
sqrt(x)/(x + 1)Кубический корень
cbrt(x)/(3*x + 2)С применением синуса и косинуса
2*sin(x)*cos(x)Арксинус
x*arcsin(x)Арккосинус
x*arccos(x)Применение логарифма
x*log(x, 10)Натуральный логарифм
ln(x)/xЭкспонента
exp(x)*xТангенс
tg(x)*sin(x)Котангенс
ctg(x)*cos(x)Иррациональне дроби
(sqrt(x) - 1)/sqrt(x^2 - x - 1)Арктангенс
x*arctg(x)Арккотангенс
x*arсctg(x)Гиберболические синус и косинус
2*sh(x)*ch(x)Гиберболические тангенс и котангенс
ctgh(x)/tgh(x)Гиберболические арксинус и арккосинус
x^2*arcsinh(x)*arccosh(x)Гиберболические арктангенс и арккотангенс
x^2*arctgh(x)*arcctgh(x)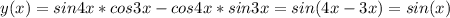
есть 
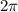
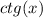равен 
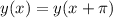
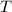- искомый период, тогда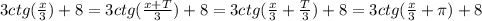
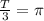
относительно оси OX на 8 единиц вверх, также не влияя на период
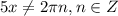
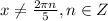
- это симметричное относительно начала координат множество точек,
также симметрична относительно начала координат. Это означает, что есть смысл проверять функцию на парность, дальше.
ответ: x=-3.
Объяснение:
√(x+28)=2-x
ОДЗ: x+28≥0 x≥-28 2-x≥0 x≤2 ⇒ x∈[-28;2].
(√(x+28))²=(2-x)²
x+28=4-4x+x²
x²-5x-24=0 D=121 √D=11
x₁=-3 x₂=8 ∉ ОДЗ.