25.378
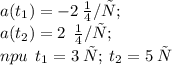
25.379
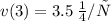
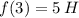
Объяснение:
Указанный закон
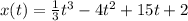
описывает функциональную зависимость расстояния х от времени t
Скорость тела v(t) определяется как производная от функции расстояния в заданный момент времени t
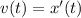
Ускорение тела a(t) определяется как производная от функции скорости v(t) в заданный момент времени t,
соответственно, ускорение будет определяться как производная второго порядка от функции расстояния в заданный момент времени t
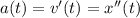
Моментом(ами), когда скорость тела равна нулю, будут такие моменты времени t, при которых будет соблюдаться равенство:
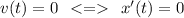
Вычислим значение t, для которого v(t)=0.
Для этого найдем функцию скорости v(t) как производную x(t):
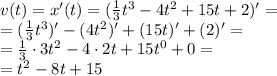
Приравняем полученное к нулю:
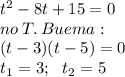
Нами получено 2 момента времени, когда скорость тела равна нулю.
Наййдем ускорение тела в вычисленные моменты времени.
Ускорение тела a(t) определяется как производная от функции скорости v(t) в заданный момент времени t,
поэтому вначале найдем производную
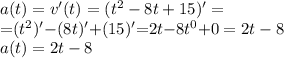
Затем вычислим ее значение в полученные моменты времени:
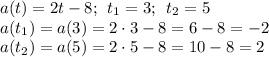
Примечание:
отрицательное значение ускорения - это означает, что вектор ускорения направлен в обратную сторону относительно вектора направнения движения (т.е. это торможение)
25.379
x(t)=\frac{t^3}{6}-\frac{t^2}{4}+\frac{t}{2}+5x(t)=
6t ^3 − 4t ^2 + 2t+5
1. Найдем скорость в момент времени t=3
- определим функцию скорости v(t), вычислив производную x'(t):
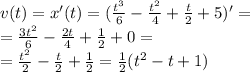
- найдем значение v(t) в заданный в условии момент времени t=3
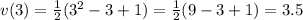
Получили ответ на 1-й вопрос задачи:
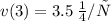
2. Определим значение силы f, действующей на тело, в момент времени t=3.
Как известно, сила рассчитывается как произведение массы тела на его ускорение в конкретный момент времени a(t):
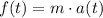
Ускорение тела a(t) определяется как производная от функции скорости v(t) в заданный момент времени t
(также это - производная второго порядка от функции расстояния):
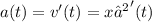
Вначале определим функцию ускорения тела в момент времени t.
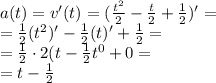
Определим значение силы f, действующей на тело, в момент времени t=3 (масса из условия равна 2 кг):.
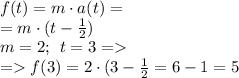
Получили ответ на 2-й вопрос в задаче:
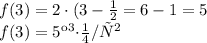
или, т.к. 1 кг•м/с² - это 1 Н (по определению)
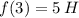
-----------------
X^2/y +y^2/x=3 ;x+y=2 решите систему
-----------------------------
{ x²/y +y²/x = 3 ; x+y =2 .⇔{ (x³ +y³)/xy =3 ; x+y =2 . ⇔
{ ( (x+y)³ -3xy(x+y) ) /xy =3 ; x+y =2. ⇔{ ( 2³ -3xy*2 )/xy =3 ; x+y =2. ⇔
{ xy =8 /9 ; x+y =2.
* * *x и y корни уравнения t²-2t +8/9 =0 →обратная теорема Виета * * *
дальше "традиционно" :
{ xy =8 /9 ; y =2 -x.
x(2-x) =8/9 ;
2x -x² =8/9 ;
x² -2x +8/9 =0 ! * * * t² -2t +8/9 =0 * * *
x₁ ₂ = 1±√(1 -8/9) ;
x₁ ₂ = 1 ±√(1/9) ;
x₁ ₂ = 1 ±1/3 ;
x₁= 1 -1/3 =2/3 ⇒ y₁ =2 -x₁ = 2 -2/3 =4/3 ;
x₂ = 1+1/3 =4/3 ⇒ y₂ =2 - x₂ = 2 -4/3 =2/3.
* * * уравнения системы симметричные * * *
ответ: (2/3 ; 4/3) , (4/3 , 2/3) .
--------------
Удачи !