Действительных корней нет.
Комплексные корни:
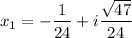
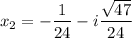
Объяснение:
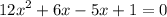
Приводим подобные слагаемые:
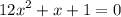
Это обычное квадратное уравнение. Решим через дискриминант.
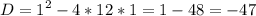
Дискриминант меньше нуля, следовательно действительных корней нет.
Найдем комплексные корни.
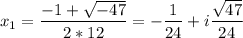
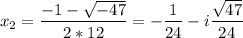
Теория:
Стандартный вид квадратного уравнения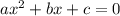 
, 
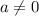
Дискриминант 
Если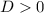 
, то квадратное уравнение имеет два действительных корня.
Если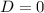 
, то квадратное уравнение имеет один действительных корень.
Если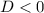 
, то квадратное уравнение не имеет действительных корней, однако комплексные корни существуют.
Комплексное число - число вида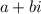 
, где 
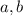- действительные числа, 
- мнимая единица.
Мнимая единица - число, для которого выполняется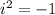 
-3а>-3b ⇒ делим на (-3) и знак меняем на противоположный a < b
1) a< b
2) 2/7a< 2/7b умножили верное неравенство a < b на 2/7 - положительное число, знак неравенства не изменился
3) b-4 > a-4
верное неравенство b > a от обеих частей отняли поровну 4, знак неравенства не изменился
4) -5/9b < -5/9a
умножили верное неравенство b < a на(-5 /9 - отрицательное число, знак неравенства изменился
5)3a+2 < 3b+2
Умножили верное неравенство
a < b на 3 - положительное число, знак неравенства не изменился
и потом прибавили поровну число 2 и слева и справа
6) -5a+10> -5b+10
умножили верное неравенство a < b на (-5) - отрицательное число, знак неравенства изменился
Потом прибавление к обеим частям неравенства 10 не меняет знак.
а) 5х+6х-5-18>0⇒11х>33 x>3
0.6х-1<3.2⇒x<7
x∈(3;7)
б) 3х+4х<12⇒x<12/7; 12/7=1 5/7
-2x>-3⇒x<1.5
х∈(-∞;1.5)