14 ч 20 мин - 14 ч = 20 мин = 20/60 ч = 1/3 ч - время движения до встречи;
20 : 1/3 = 20 · 3/1 = 60 км/ч - скорость сближения
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Пусть х км/ч - скорость велосипедиста, тогда (60 - х) км/ч - скорость мотоциклиста. На следующий день мотоциклист был в пути 24 мин = 24/60 ч = 2/5 ч, а велосипедист был в пути (24 - 16) = 8 мин = 8/60 ч = 2/15 ч. Расстояние между ними по прежнему 20 км. Уравнение:
2/15 · х + 2/5 · (60 - х) = 20
2/15х + 24 - 2/5х = 20
2/15х - 6/16х = 20 - 24
-4/15х = -4
х = -4 : (-4/15) (-) : (-) = (+)
х = 4 · 15/4
х = 15
ответ: 15 км/ч.
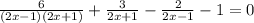
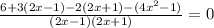
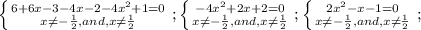
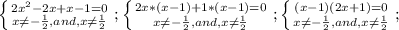
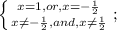
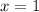
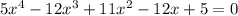
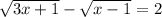
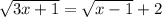 ,
, 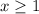
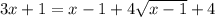 ,
, 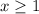
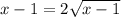 ,
, 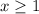
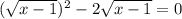 ,
, 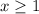
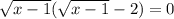 ,
, 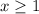
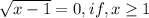
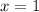
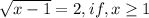
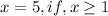
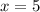
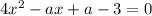
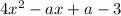 - парабола ветками вверх, нам нужен случай, когда вершина параболы лежит на оси ОХ, т.е. когда парабола пересекает эту ось в одной точке.
- парабола ветками вверх, нам нужен случай, когда вершина параболы лежит на оси ОХ, т.е. когда парабола пересекает эту ось в одной точке.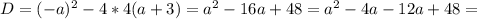
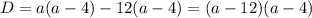
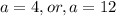
Раз x≠{-2;3}, то у гиперболы будут выколоты точки (-2;-0,5), (3;1/3).
Таблицу точек для построения и график смотри внизу.
Прямая y=kx, так же симметрична относительно начала координат, поэтому прямая будет имеет только одну общею точку с графиком, когда она проходит через одну выколотую точку. По координатам выколотых точек, можно заметить что они не симметричны относительно (0;0), поэтому прямая y=kx не может проходить через них одновременно. Найдём k.
ответ: 1/9 и 0,25.