Определим в каких четвертях располагаются углы 2, 4 и 6 радиан:
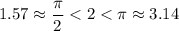
Угол в 2 радиана принадлежит 2 четверти.
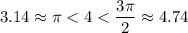
Угол в 4 радиана принадлежит 3 четверти.
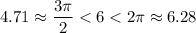
Угол в 6 радиан принадлежит 4 четверти.
Рассмотрим выражения:
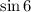 - синус в 4 четверти принимает отрицательные значения
- синус в 4 четверти принимает отрицательные значения
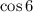 - косинус в 4 четверти принимает положительные значения
- косинус в 4 четверти принимает положительные значения
Сразу отметим, что разность  отрицательна, так как из отрицательного числа вычитается положительное
отрицательна, так как из отрицательного числа вычитается положительное
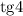 - тангенс в 3 четверти принимает положительные значения
- тангенс в 3 четверти принимает положительные значения
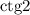 - котангенс во 2 четверти принимает отрицательные значения
- котангенс во 2 четверти принимает отрицательные значения
Итак, у нас есть 3 сомножителя знаки которых нам известны:
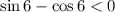
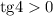
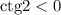
Произведение двух отрицательных и одного положительного числа положительное:

ответ: знак (+): выражение положительно
Чтобы изобразить график линейной функции вида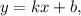 где
где 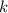 и
и 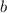 — коэффициенты, достаточно на координатной плоскости отметить две точки и провести через них прямую.
— коэффициенты, достаточно на координатной плоскости отметить две точки и провести через них прямую.
Для этого строят таблицу для двух точек: первая строка — абсцисса (иксы), вторая строка — ордината (игреки). Вы — хозяин своей таблицы. Подбирайте любое значение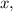 подставляйте его в функцию и находите
подставляйте его в функцию и находите 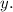 (Подбирайте числа в пределах разумного.)
(Подбирайте числа в пределах разумного.)
Пример. Изобразить график линейной функции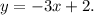
Строим таблицу для двух точек:
Пусть
Тогда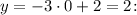
Пусть
Тогда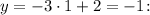
Имеем заполненную таблицу для двух точек. Изобразим координатную плоскость, отметим две точки: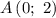 и
и 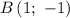 — и проведем через них прямую (см. вложение). График линейной функции
— и проведем через них прямую (см. вложение). График линейной функции 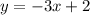 построен.
построен.