Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
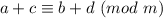
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
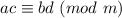
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
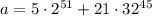
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,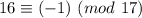 
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что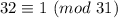 
, получаем
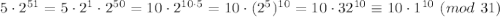
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
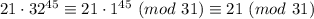
Остаток 21, чудесно. Выполняем последний шаг.
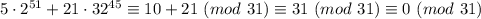
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
Монотонная функция -функций, у которой одному значению переменной соответствует только одно значение функции.
Пойдем методом от противного
пусть в точках х и х+с функция принимает одно и то же значение, тогда:
x^3=(x+c)^3
x^3=x^3+3x^2c+3xc^2+c^3
3c *x^2+ 3c^2 *x +c^3=0|:c не равное 0
3x^2+3cx+c^2=0
D=9c^2-4*3c^2=-3c^2<0
Значит не существует такого с, что функция в при нескольких икс принимает одно и то же значение, а значит она монотонна.
Если функция монотонна, то достаточно доказать, что если функция f(х+1) больше функции f(x) -то функция явл возрастающей.
Пусть:
(x+1)^3>x^3
x^3+3x^2+3x+1>x^3
3x^2+3x+1>0
D=9-12=-3<0
Значит уравнение корней не имеет, у параболы ветви вверх, значит она всюду больше 0
Отсюда следует, что:
(x+1)^3>x^3
f(x+1)>f(x)
Значит функция является монотонно возрастающей.