Дана функция 
Её можно дать так: y = (2^x)²-a*2^x + 4. Заменим 2^x = m.
y = m² - am + 4.
Производную приравняем нулю: y' = 2m - a = 0. a = 2m.
Полученное значение подставим в выражение функции, которая должна быть равна 3.
m² -2m*m + 4 = 3.
Отсюда получаем m² = 1, тогда m = +-1. Отрицательное значение неприемлемо (2 в любой степени не может быть отрицательным).
Обратная замена: 2^x = 1 или 2^x = 2^0.
Найдена абсцисса,в которой функция равна 3.
Теперь находим значение а = 2m = 2*1 = 2.
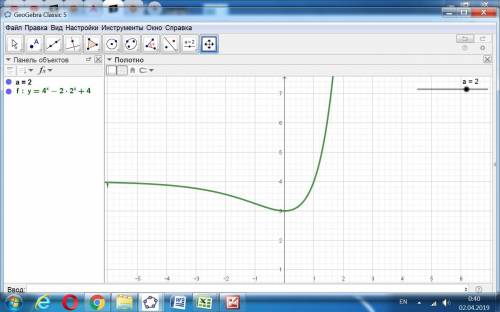
Уравнение функции, минимум которой равен 3:
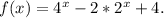
1). Второе слагаемое умножается и делится на 2. В результате получается удвоенное произведение b/2a и х. Так как квадрат х представлен в качестве первого слагаемого, то для полного квадрата суммы не хватает квадрата второго слагаемого, то есть (b/2a)².
Добавляем этот недостающий элемент и, чтобы значение выражения не изменилось, - вычитаем его же.
c/a оставляем без изменений:
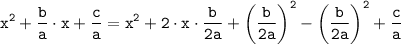
2). Записываем получившийся полный квадрат суммы:
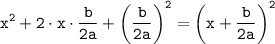
Оставшиеся два слагаемых группируем со сменой знака:
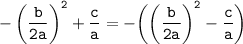
Приводим выражение в скобках к общему знаменателю 4а²:
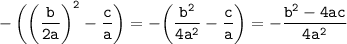
3). Получаем в результате:
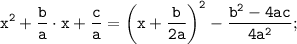
1x - y = -2
1x + y = 3
(1x - y) + (1x + y) = -2 + 3
1x - y + 1x + y = 1
2x = 1
x = 0,5
0,5 + y = 3
y = 2,5
ответ: (0,5; 2,5).