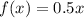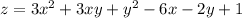
1. Градиент - это вектор вида 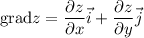 .
.
Найдем частные производные:
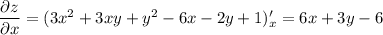
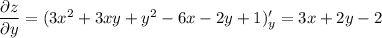
Найдем значение частных производных в точке А:
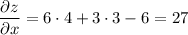
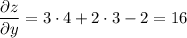
Градиент принимает вид:
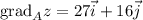
2. Производная по направлению вектора 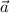 определяется как
определяется как 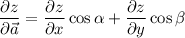 , где
, где 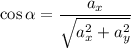 ,
, 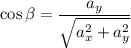
Определим направляющие косинусы:
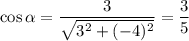
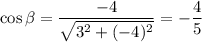
Значения частных производных в точке А уже вычислялись. Вычисляем производную по направлению:
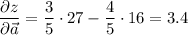
3. Необходимое условие экстремума: равенство нулю частных производных. Приравняем частные производные к нулю, составим и решим систему:
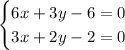
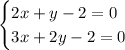
Выразим из первого уравнения у:
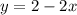
Подставим во второе:
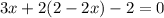
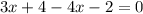
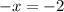
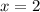
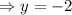
Таким образом, точка (2; -2) - предполагаемая точка экстремума.
Найдем вторые производные функции:
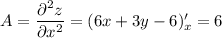
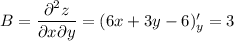
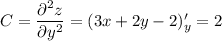
Рассмотрим выражение 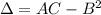 :
:
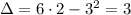
Так как 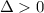 и
и 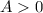 , то (2; -2) - точка минимума.
, то (2; -2) - точка минимума.
Найдем значение минимума:
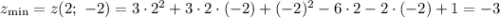
а) 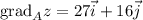
б) 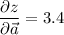
в) 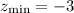
Искомая функция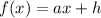 .
.
Найдем значения искомой функции в заданных точках х:
Кроме этого, для каждого из аргументов х есть еще и экспериментальное значение, которое обозначим через функцию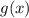 :
:
Составим функцию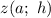 , которая будет суммировать квадраты разностей значений функций
, которая будет суммировать квадраты разностей значений функций 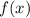 и
и 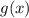 соответствующих аргументов:
соответствующих аргументов:
Исследуем эту функцию на экстремумы.
Найдем частные производные:
Необходимое условие экстремума - равенство нулю частных производных. Составим систему:
Домножим второе уравнение на (-3):
Складываем уравнения:
Подставим значение а во второе уравнение исходной системы:
Точка (0.5; 0) - предполагаемая точка экстремума.
Найдем вторые частные производные функции:
Рассмотрим выражение:
Так как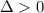 и
и 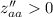 , то точка (0.5; 0) является точкой минимума.
, то точка (0.5; 0) является точкой минимума.
Значит, в точке (0.5; 0) функция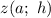 имеет минимум.
имеет минимум.
Тогда, значения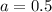 и
и 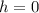 есть искомые коэффициенты функции
есть искомые коэффициенты функции 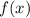 .
.
ответ: