Объяснение:
Ищем точки пересечения с осью ОХ
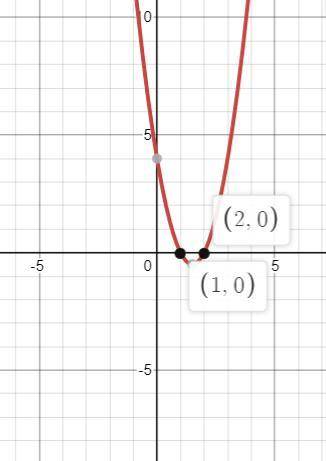
1) Ветви параболы направлены вверх, вершина x₀=-b/2а=6/4=1,5
точки пересечения с осью ОХ:
2x² - 6x + 4=0;
D=36-4*4*2=4; x₁=(6-2)/4;x₁=1;x₂=(6+2)/4;x₂=2
x∈(1;2)
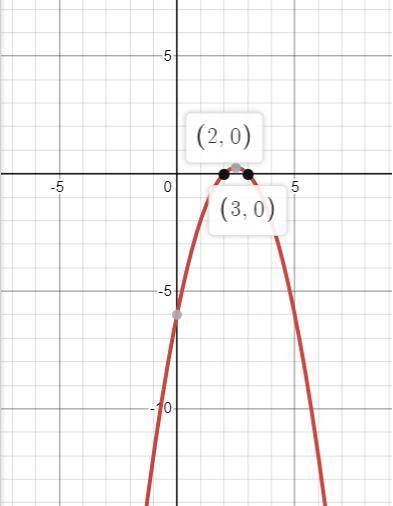
2) Ветви параболы направлены вниз ,вершина x₀=-b/2а=5/2=2,5
точки пересечения с осью ОХ:
x² -5x + 6=0; по т. Виета x₁=2; x₂=3
х∈(-∞;2)∪(3;∞)
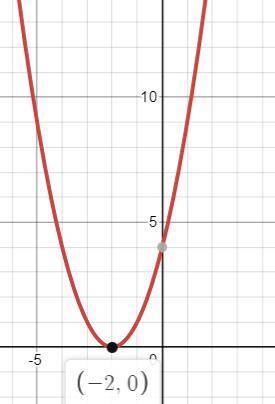
3)y = x² + 4x + 4; y=(х+2)²
y=(х+2)²=0; х=-2. Пересечение в одной точке и это же вершина
х∈∅
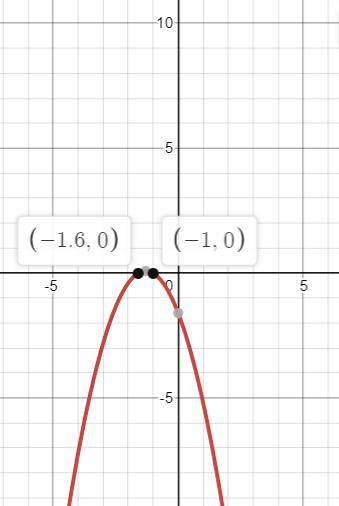
4) Ветви параболы вниз. Вершина x₀=-b/2а=2,6/2=1,3
точки пересечения с осью ОХ: x² + 2,6x + 1,6=0;
По т. Виета x₁=-1,6; x₂=-1.
х∈(-∞;-1,6)∪(-1;∞)
Дискриминант больше нуля - два корня
Дискриминант равен нулю. В уравнении 1 корень
Дискриминант меньше нуля, значит нет действительных корней
2)
Найти область определения функции - это найти "проблемные точки" в функции, при которых функция перестанет существовать.
В нашем случае, это нельзя допускать, когда знаменатель обратится в ноль. Для этого мы должны его приравнять к нулю и выяснить, при каких значениях функция перестанет существовать.
В нашем случае функция не имеет смысла, при х=-1 и х=0