1) Обозначим первую цифру задуманного числа х, а вторую - у. Выполнив указанные действия, получим:
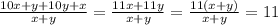
Т.е., всегда будет получаться 11.
2) Признак делимости на 3: на три делятся те числа, сумма цифр которых делится на 3.
Данное число (10^n+317) будет состоять из единицы, n нулей, тройки, единицы и семёрки. Сумма цифр равна 1+3+1+7 = 12.
12 делится на 3, значит, и число 10^n+317 тоже делится на 3, ЧТД
Аналогично, признак делимости на 9: на 9 делятся те числа, сумма цифр которых делится на 9.
10^n состоит из единицы и n нулей. Если от него отнять 1, оно будет состоять из девяток. Соответсвенно, сумма цифр этого числа поделится на 9, ЧТД.
х⁴+ 3x³ - 8x² + 3x + 1=0
получили симметрическое уравнение четвертой степени, т.к. х≠0, то разделив обе части на х², получим х²+3х-8+3/х+1/х²=
((х+1/х)²-2)+3(х+1/х)-8=0
замена (х+1/х)=у, тогда у²+3у-2-8=0
у²+3у-10=0, По Виета у=-5, у=2
Значит, х+1/х=-5 или х+1/х=2,
х⁴+ 3x³ - 8x² + 3x + 1=(х²-2х+1)(х²+5х+1)=
(х-1)²(х²+5х+1)=(х-1)²(х-(-2.5+√5.25))(х-(-2.5-√5.25))=
(х-1)²(х+2.5-√5.25))(х+2.5+√5.25)
х²+5х+1=0
х=-2.5±√(6.25-1)=(-2.5±√5.25)
ВТОРОЙ ВО ВЛОЖЕНИИ