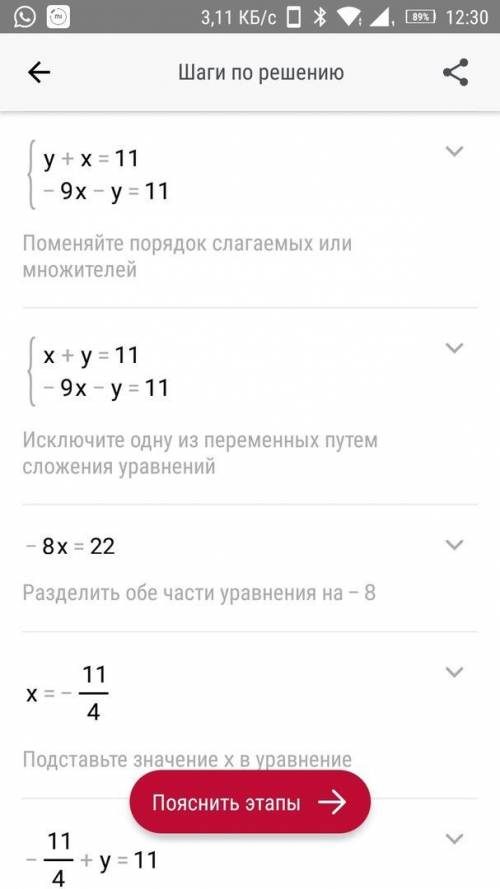
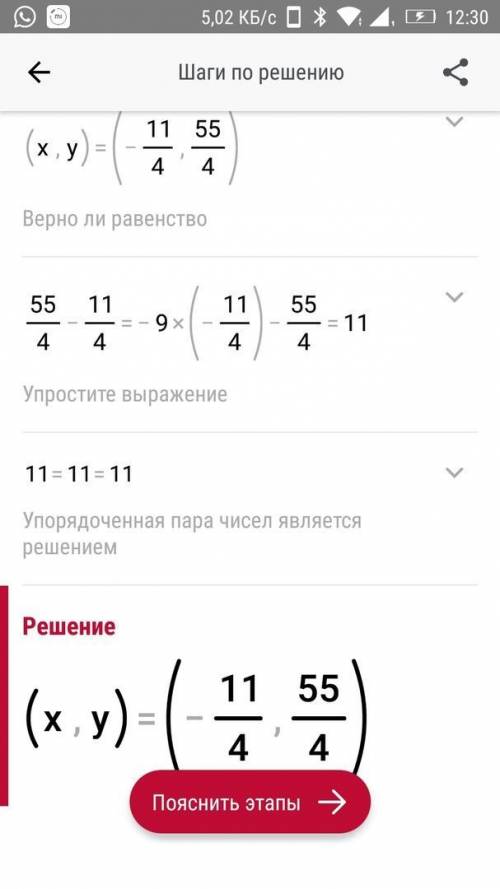
(х,y)=(-11\4)-55\4=11
Объяснение:
17см
Объяснение:
Позначимо гіпотенузу буквою х. Тоді перший катет дорівнює (х - 9) см. Другий катет на 7 см більше першого: х - 9 + 7 = х - 2 (см).
Площа прямокутного Трикутник дорівнює половині твори катетів і дорівнює 60 см ², складемо рівняння: (х - 2) (х - 9) / 2 = 60.
Вирішуємо рівняння:
х² - 2х - 9х + 18 = 120.
х² - 11х + 18 - 120 = 0.
х² - 11х - 102 = 0.
Вирішуємо квадратне рівняння через дискримінант.
D = 121 + 408 = 529 (√D = 23);
х1 = (11 - 23) / 2 = -12/2 = -6 (не підходить).
х2 = (11 + 23) / 2 = 17 (см).
Відповідь: 2) гіпотенуза трикутника дорівнює 17 см.
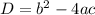(если дискриминант больше нуля уравнение имеет 2 корня, если равен нулю, уравнение имеет 1 корень, если меньше нуля, то нет корней), либо применяя разложение многочлена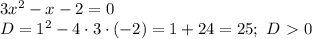
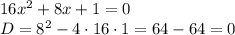
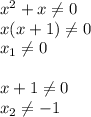
ответ:(1; -11)
это сложения
Объяснение: