ответ: y = -6x - 11
Объяснение:
Касательная параллельна прямой y = -6x + 7. Коэффициент наклона этой прямой равен -6.
Так как касательная параллельна этой прямой, следовательно, коэффициент наклона касательной тоже равен -6.
То есть мы знаем коэффициент наклона касательной, а, тем самым, значение производной в точке касания.
Итак, у нас дана функция y = x² - 4x - 10 и значение производной в точке касания.
а) Найдем точку, в которой производная функции y = x² - 4x - 10 равна -6.
Сначала найдем уравнение производной.
y' = (x² - 4x - 10)' = 2x - 4
Приравняем производную к числу -6.
2x - 4 = -6
2x = -2
x = -1
б) Найдем уравнение касательной к графику функции y = x² - 4x - 10 в точке x₀ = -1.
Найдем значение функции в точке x₀ = -1.
y(-1) = (-1)² - 4·(-1) - 10 = 1 + 4 - 10 = -5
Подставим эти значения в уравнение касательной:
y - y(x₀) = y'(x₀)(x - x₀)
y - (-5) = -6(x - (-1))
y + 5 = -6(x + 1)
y = -6x - 6 - 5
y = -6x - 11
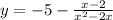
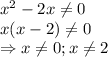
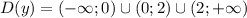
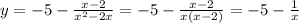
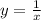, отображенную симметрично оси абсцисс и сдвинутую на 5 единиц вниз. Помним про то, что функция не определена в точках 0 и 2.
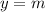представляет собой прямую, параллельную оси абсцисс, проходящую через точку (0; m). 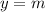не имеет общих точек с построенным графиком при 
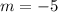(асимптота гиперболы по построению, так как сдвиг проводился на 5 единиц вниз) и при 
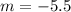(именно это значение принимала бы функция 
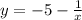в точке 2, но эта точка не принадлежит области ее определения).
Пояснення вытянуты из вазы квитку