y = x² + 2x - 8
y = x² + 2x + 1 - 9 = (x + 1)² - 9
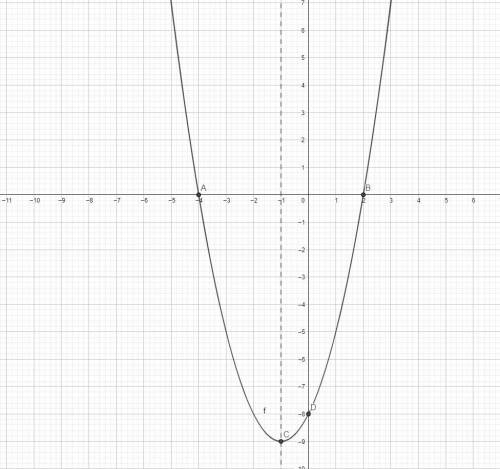
Видим, что график смещён вниз на 9 единиц и влево на 1 единицу. Соответственно, вершина данного графика будет с координатами: (-1; -9).
Найдём точки пересечения с осью OX, решив уравнение: x² + 2x - 8 = 0.
По т-ме Виета корни: -4; 2. То есть, график пересекает ось ОХ в точках (-4; 0) и (2; 0).
График также проходит через точку (0; -8) - это характерная точка (то есть, если подставить 0 вместо х, мы получим лишь свободный член, это -8).
Ось симметрии: x = -1.
Строим график по полученным точкам.
функцию можно записать так: y = (1 / 3)x - 4x^(- 2) + √x.
воспользовавшись формулами:
(x^n)’ = n* x^(n-1) (производная основной элементарной функции).
(√x)’ = 1 / 2√x (производная основной элементарной функции).
(с * u)’ = с * u’, где с – const (основное правило дифференцирования).
(u + v)’ = u’ + v’ (основное правило дифференцирования).
таким образом, производная нашей функции будет следующая:
y' = (x / 3 – 4 /x ^2 + √x)’ = ((1 / 3)x - 4x^(- 2) + √x)’ = ((1 / 3)x)’ – (4x^(- 2))’ + (√x)’ = (1 / 3 ) – (4 * (- 2) * x^(- 2 - 1)) + (1 / 2√x) = (1 / 3 ) + 8x^(- 3)) + (1 / 2√x) = (1 / 3 ) + (8 / x^3) + (1 / 2√x).
ответ: y' = (1 / 3 ) + (8 / x^3) + (1 / 2√x).