Даны координаты вершин пирамиды KLMN: K(10;6;6), L2;8;2), V(6;8;9), N(7;10;3).
Найти:
1)Длину ребра KL;
2)Угол между ребрами KL и MN;
3)Уравнение прямой KL.

Question

Алгебра: Даны координаты вершин пирамиды KLMN: K(10;6;6), L2;8;2), V(6;8;9), N(7;10;3). Найти: 1)Длину ребра KL; 2)Угол между ребрами KL и MN; 3)Уравнение прямой KL.

SuperLeonellus123 · Accepted Answer

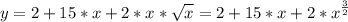
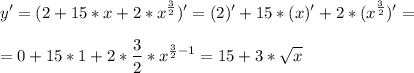
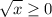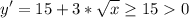
Нет точки максимумаОбъяснение:Рассмотрим функцию Так как в составе функции участвует квадратный корень, то область определений функции: x≥0, то есть D(y)=[0; +∞).Чтобы найти экстремумы (локальные минимумы и максимумы) будем исследовать функцию с производной функции. Вычислим производную функции:Так как , тодля любого x∈D(y). Это означает, что данная функция монотонно возрастает в D(y). Отсюда следует, что у функции нет точки максимума.Так как функция монотонно возрастает в D(y), то минимальное значение...

Даны координаты вершин пирамиды KLMN: K(10;6;6), L2;8;2), V(6;8;9), N(7;10;3). Найти: 1)Длину ребра KL; 2)Угол между ребрами KL и MN; 3)Уравнение прямой KL.

MOGZ ответил

Даны координаты вершин пирамиды KLMN: K(10;6;6), L2;8;2), V(6;8;9), N(7;10;3).
Найти:
1)Длину ребра KL;
2)Угол между ребрами KL и MN;
3)Уравнение прямой KL.