Объяснение:
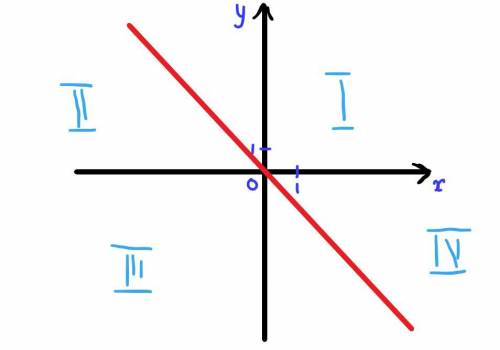
y = -x
1) Функция имеет единственный ноль к точке (0, 0)
2) Область определения функции ( -∞ ; +∞)
3) Область значений такая же, т.е. ( -∞ ; +∞)
4) Область определения совпадает с областью значений
5) Функция располагается в 2 и 4 четвертях
6) Функция положительна ТОГДА И ТОЛЬКО ТОГДА, когда её аргумент отрицателен
7) Функция отрицательна ТОГДА И ТОЛЬКО ТОГДА, когда её аргумент положителен
8) Это монотонно убывающая функция
9) Функция убывает на всей своей области определения
10) Функция не имеет периода
11) График этой функции - прямая, проходящая через центр координат
12) Это нечётная функция
13) Тангенс угла наклона касательной к точке графика постоянен и равен -1 для всех х
14) Площадь под графиком от 0 до х равна 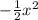
Здесь все свойства функции, выбирайте нужные.
На графике красным - сам график
Голубым подписаны четверти, их подписывать не обязательно.
Объяснение:
220. Выделим квадрат двучлена:
=a) 2x²−3x + 7 = 2(x³²− 2¹ x + x+ 3 7 2 GOZP2MA.INFO
GUZPUTINA.INFO
GUZPU
GOZPU
GUZPU
GOZPU
= 2(x²-2·x· ²³ +₁ + 27/2 = - 2((x-2²-47)=2(x-2)²2-5² ². 3 9 9 4 16 16 2 GOZPUTINA.INFO 16 GUZPUTINA.INFO
4 -ó) −3x² + 4x−1 = −3(x² - ²x + x + — — ) = −3(x³²-2.x. GD + 4 4 - —— +-) 99 3
= -3((x - ²)²) = -3(x-²)² + 3 GUZE 9 MA
GUZPUTINA.INFO
GUZPUTINA.IN −b) 5x²-3x = 5(x²_²_x) = S(x = 5(x²-2x. GOZPUTINA.INFO 3 9 9 + ) = 5((x—_²_) ²__ 9 100 GOZPUTINA.INFO
GOZPUTINA.INFO 10 20
GOZPUTINA.INFO
r) -4x² + 8x = 4(x²-2x) = -4(x²-2·x·1+1−1) = -4((x-1)²-1) = -4(x-1)² + 4.

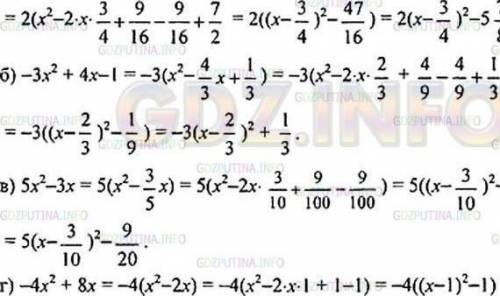

х1=0
х2=1/2
Объяснение:
Решение в приложении