1.В соревнованиях по баскетболу участвовало 14 команд. Каждая команда провела с каждой из остальных по одной игре на своем поле и по одной игре на поле противника. Сколько всего игр сыграно?
2.Из цифр 0,2,3,5 составили все возможные варианты четырехзначного числа (без повторения цифр). Сколько среди них таких чисел, которые больше 2000, но меньше 5000.
3. На странице альбома 13 свободных мест для фотографий. Сколькими можно вложить в свободные места 3 фотографии?
4. В ящике находятся шары с номерами 1,2,3,4….10. Наугад вынимают один шар. Какова вероятность того, что номер этого шара будет четным числом?
5. По списку В 9 классе 15 девочек и 13 мальчиков. Сколькими можно выбрать 3 мальчиков и 2 девочек для работы в библиотеке?
6.На четырех карточках написаны цифры 1,3,5,7. Карточки перевернули и перемешали. Затем наугад последовательно разложили эти карточки в ряд одну за другой и открыли. Какова вероятность того, что в результате получится число большее 5000?
Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру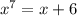
уравнение в действительных корнях.
Рассмотрим функцию
. Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию
. Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.