tg2x-sec2x
Объяснение:
умножим числитель и знаменатель первой дроби на sinx-cosx
тогда числитель (sinx-cosx)²,знаменатель sinx²-cosx²
Раскроем числитель по ФСУ тогда sinx²+cosx²-2sinxcosx, а в знаменателе вынесем -1, тогда cosx²-sinx² по ОТТ и формуле двойного угла для синуса числитель равен 1-sin2x, а знаменатель по формуле двойного угла для косинуса равен -cos2x. Почленно поделим на -cos2x, тогда получим tg2x-1/cos2x, по определению, величина обратная косинусу есть секанс, окончательно получаем tg2x-sec2x
1)
По теореме Виета для уравнения 4х²-6х-1 :
х1+х2 = 1.5
х1*х2 = -0.25
2)
По теореме Виета для нового уравнения :
В = -(у1+у2) = -((2/х1³)-1 +(2/х2³)-1) = 578
С = -(у1*у2) = ((2/х1³)-1)*((2/х2³)-1) = 321
Уравнение : y²+578y+321 = 0
ответ : у²+578у+321 = 0
P.S если интересно как я из -((2/х1³)-1 +(2/х2³)-1) получил 578, то я сейчас примерно покажу (для удобства пусть х1 будет х, а х2 будет у) :
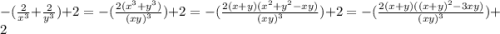
Ну и уже по теореме Виета (х+у = 1.5, х*у = -0.25) я подставил значения и решил, с умножением там примерно тоже самое)
ответ: 0 ≤ x ≤ 1
Объяснение: Я спростив вираз таким чином. Домножимо ліву і праву частину нерівності на 2ˣ. Основа степенної функції більше за 1, тож знак нерівності не зміниться.
(2ˣ+2¹⁻ˣ)·2ˣ≤3·2ˣ
2²ˣ+2¹⁻ˣ⁺ˣ-3·2ˣ≤0
(2ˣ)²-3·2ˣ+2≤0, зробимо заміну z=2ˣ
z²-3z+2≤0, знадемо корені рівняння z²-3z+2=0, D=9-4·2=1, z₁=1, z₂=2
На числовій прямій відкладемо z₁=1, z₂=2. За до методу інтервалів знайдемо рішення нерівності z²-3z+2≤0.
+ - +
12 z ∈ [1;2]
Або 1 ≤ z ≤ 2. Зворотня заміна. Знову повторюсь: через те що основа степеня більша за 1, знаки нерівності зберігаються.
1 ≤ z ≤ 2
1 ≤ 2ˣ ≤ 2
2⁰ ≤ 2ˣ ≤ 2¹
0 ≤ x ≤ 1