Найдем решения неравенства Ix-5I≤2; -2≤х-6≤2; 4≤х≤8- отрезок длиной 4
Найдем решения неравенства Ix-6I≥1
x-6≥1; х≥7 или х-6≤-1; х≤5; т.е. х∈(-∞;5]∪[7;8]
Из отрезка [4;8] выпадает только отрезок[5;7] длины 2
Используя геометрическое определение вероятности, найдем искомую вероятность, длина решений второго неравенства, которое находится в первом, составляет 2, это сумма длин отрезков [4;5] и [7;8], т.е. число благоприятствующих исходов равно 2, а общее число исходов 4, значит, вероятность равна 2/4=0.5
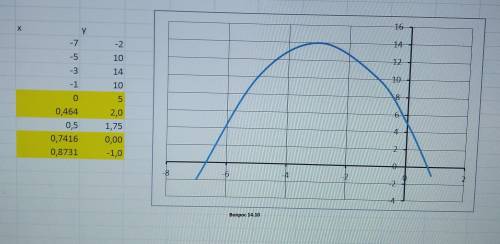
14.10
1) f(0)=5; f(0,464)=2; f(-6,873)=-1
2) ) f(-6,742)=0; ) f(0,7416)=0
Функция положительная при -6,742< х<0,7416
3) Вершина параболы при х= -3 Ось симметрии х=-3
4) наибольшее значение f(-3)=14
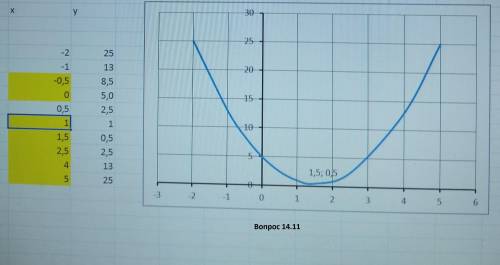
14.11
1) Вершина параболы при х= 1,5 Ось симметрии х=1,5
2) наименьшее значение f(1,5)=0,5 множества значений f(х)≥0,5
3) Промежутки возрастания х>1,5
Убывания х< 1,5
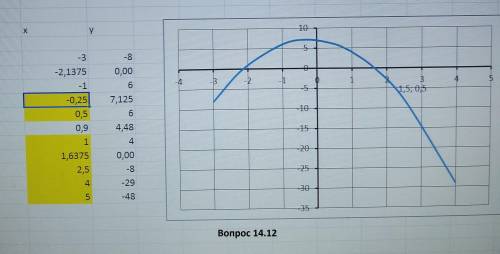
14.12
1) Вершина параболы при х= -0,25 Ось симметрии х=-0,25
2) наибольшее значение f(-0,25)=7,125
множества значений f(х)≤ 7,125
Промежутки возрастания х<-0,25
Убывания х>-0,25
Объяснение:
х2≤ 1/4
|х|≤ 1/2
х ≤ 1/2,х ≥ 0
-х ≤ 1/2, х<0
х є [0, 1/2]
х ≥ -1/2, х<0
х є [0, 1/2]
х є [-1/2,0]
х є [-1/2;1/2]
б) х2+3х-2х-6>0
х*(х+3)-2(х+3)>0
(х+3)*(х-2)>0
{х+3>
{х-2>0
{х+3<0
{х-2<0
{х>-3
{х>2
{х<-3
{х<2
х є (2;+ ∞ )
х є (- ∞ ; -3)
в)
{2х-3 ≤0
{х+4>0
{2х-3 ≥ 0
{х+4<0
{х ≤ 3/2
{х>-4
{х≥ 3/2
{ х<-4
х є (-4;3/2]
г) х2+х+х-1≥0
-х*(х-1)+1(х-1) ≥0
-(х-1)*(х-1) ≥0
-(х-1)2 ≥ 0
(х-1)2 ≤ 0
(х-1)2=0
х=1