Объяснение:
1а) x² + x - 20 ≠0
найдем x² + x - 20 = 0
D = 1+80 = 81
x ₁ ₂ = (-1 ±9) / 2
x₁ = -5
x₂ = 4
ОВФ (-∞; -5)∩ (-5;4)∩(4; +∞)
1б) получитсясистема:
{x+9 ≥0 {x≥-9
{4-x ≥0 {x ≤4
ОВФ [-9;4]
2a) f(-x) = -4x⁷ +2x³ = -f(x) нечетная
2б) f(-x) = (-x)² -3(-x)⁴= x² -3x⁴ = f(x) четная
2в) f(-x) = -x³ + (-x)⁶ = -x³ + x⁶ ≠ f(x) ≠ f(x) ни четная, ни нечетная
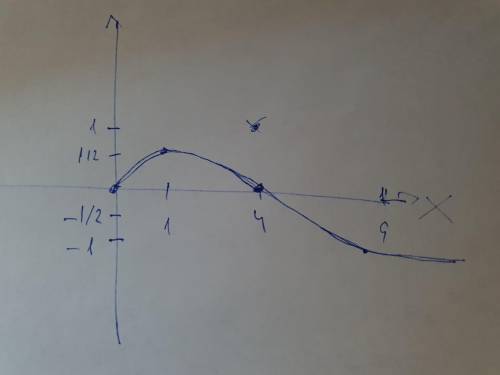
3) область определения X≥0
а) пересечение с x т. е. y =0 при х = 0 и x = 4 точки (0;0), (4;0)
б) возрастание [0;1]
убывание (1;+∞)
в) ОЗФ, [0.5; +∞)
а) 10ху^2-35x^3y^3=5xy^2(2-7x^2y)
б) 9a^6 + 12a^3b^4=3a^3(a^3+4b^4)
в) 24m^2n^5 - 16m^2n^3=4m^2n^3(6n^2-4)
г) 7b^3c^3 + 14b^4c^2=7b^3c^2(c+2b)
а) 21*12 + 21*14 + 26*79=21(12+14)+26*79=21*26+26*79=26(21+79)=26*100=2600
б) 4,3*2,8 - 3,8*1,2 - 2,8*3,1= 4,3*2,8 - 2,8*3,1 - 3,8*1,2 =
= 2,8(4,3 - 3,1) - 3,8*1,2 = 2,8*1,2 - 3,8*1,2 = 1,2(2,8 - 3,8)= 1,2*(-1) = -1,2