Вообще область значений тангенса и котангенса - все действительные числа:
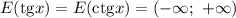
а)
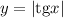
Если рассмотреть модуль тангенса, то отрицательные значения примут противоположные значения, то есть станут положительными. Нулевое и положительные значения сохранятся. Получим область значений:
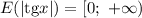
б)
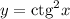
Котангенс может принять значение любого действительного числа, но при возведении любого числа в квадрат результат получится неотрицательным.
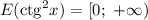
в)
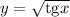
Тангенс может принять значение любого действительного числа. Под знак корня из них можно записать любое неотрицательное, при этом в результате может получиться любое неотрицательное число.
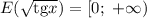
г)
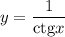
Котангенс может принять значение любого действительного числа. При делении 1 на любое число (отличное от нуля) может получиться любое число, кроме нуля.
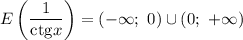
В решении.
Объяснение:
Рис. 1
1) Координаты вершины параболы (2; -1);
2) Уравнение оси симметрии: а = 2;
3) Нули функции - координаты точек пересечения параболой оси Ох, где у = 0:
(1; 0); (3; 0).
4) Функция возрастает при х∈(2; +∞);
функция убывает при х∈(+∞; 2).
5) Область значений функции - это проекция графика на ось Оу.
Обозначение Е(f) или Е(y).
Область значений параболы ограничена ординатой её вершины, у= -1.
у может быть больше, либо равен -1.
Е(y) = у∈[-1; +∞)
6) у наиб. не существует.
у наим. = -1.
Рис. 2
1) Координаты вершины параболы (-2; 2);
2) Уравнение оси симметрии: а = -2;
3) Нули функции - координаты точек пересечения параболой оси Ох, где у = 0:
(0; 0); (-4; 0).
4) Функция возрастает при х∈(-∞; -2);
функция убывает при х∈(-2; -∞).
5) Область значений функции - это проекция графика на ось Оу.
Обозначение Е(f) или Е(y).
Область значений параболы ограничена ординатой её вершины, у=2.
у может быть меньше, либо равен 2.
Е(y) = у∈[2; -∞)
6) у наим. не существует.
у наиб. = 2.