1. В самой задаче дана формула аn = -2 + 3n², где n — натуральное число.
2. Нам нужно найти значение а5, то есть нужно подставить n = 5 в данную формулу и вычислить результат.
3. Подставляем n = 5 в формулу аn = -2 + 3n²:
а5 = -2 + 3 * 5²
Делаем вычисления:
а5 = -2 + 3 * 25
а5 = -2 + 75
а5 = 73
Таким образом, a5 = 73.
Теперь взглянем на каждый шаг по-отдельности, чтобы лучше понять, как мы получили ответ 73.
1. Дана формула аn = -2 + 3n². Это означает, что для каждого натурального числа n мы можем найти соответствующее значение аn, подставив n в эту формулу.
2. Мы знаем, что нам нужно найти значение а5. Это означает, что вместо n в формуле мы будем использовать число 5, то есть n = 5.
3. Подставляем n = 5 в формулу аn = -2 + 3n²:
а5 = -2 + 3 * 5²
Здесь 5² означает 5 в квадрате, то есть 5 * 5, что равно 25.
Теперь продолжаем вычисления:
а5 = -2 + 3 * 25
Выполняем умножение:
а5 = -2 + 75
А затем сложение:
а5 = 73.
Таким образом, мы получили ответ: a5 = 73.
Надеюсь, что данное пошаговое объяснение помогло вам понять, как решить данную задачу. Если у вас возникнут еще вопросы, не стесняйтесь задавать их!
Для решения этой задачи, давайте взглянем на рисунок:
```
М-----К-----С
/ \
/ \
А ----------------- Д
```
Согласно условию, мы знаем, что отношение отрезка АМ к отрезку МВ равно 1:1, а отношение отрезка АК к отрезку КД равно 5:3. Мы также знаем, что отрезки АВ и АД равны соответственно 2 и 8.
Шаг 1: Найдем длину отрезка МВ.
Так как отношение АМ к МВ равно 1:1, это означает, что АМ и МВ равны между собой по длине. Так как АВ равна 2, то и АМ равна 2. Значит, МВ также равно 2.
Шаг 2: Найдем длину отрезка КД.
Так как отношение АК к КД равно 5:3, мы можем записать это в виде уравнения: АК / КД = 5/3. Заменим АК и АД на известные значения: 2 / КД = 5/3. Чтобы найти КД, умножим обе стороны уравнения на КД и разделим на 5: 2 * 3 / 5 = КД. Значит, КД равно 6/5.
Шаг 3: Найдем расстояние от точки К до прямой СМ.
Для этого, мы можем воспользоваться теоремой Пифагора. Из рисунка, мы видим, что прямая СМ является гипотенузой прямоугольного треугольника МКС, а отрезок КМ является одной из катетов.
Применим теорему Пифагора: КМ^2 + МС^2 = КС^2.
Мы уже знаем, что МВ равно 2, а КД равно 6/5.
Тогда МК равен 2 + 6/5 (из-за отношения АМ : МВ = 1 : 1) = 16/5 и СК равен 6/5 (из-за отношения АК : КД = 5 : 3) = 6/5.
Теперь у нас есть все необходимые значения для применения теоремы Пифагора: (16/5)^2 + (6/5)^2 = КС^2.
Упростим эту формулу: 256/25 + 36/25 = КС^2.
Складывая числители и уничтожая общий знаменатель, получаем: 292/25 = КС^2.
Чтобы найти КС, возьмем квадратный корень из обеих сторон уравнения: КС = √(292/25).
Таким образом, расстояние от точки К до прямой СМ равно √(292/25).
Відповідь:
2![\sqrt[]{3}](/tpl/images/1255/5327/34082.png) ,
, 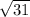 , 6,5
, 6,5
Пояснення: