y=ax²; B(-1;1/4)
1/4=a(-1)²
a=1/4
y=1/4x²; y=9
9=1/4x² /*4
x²=36
x²-36=0
(x-6)(x+6)=0
x=6 v x=-6
(-6,9) (6,9)
ответ: 3 км/ч
Пошаговое решение:
Пусть собственная скорость равна х км/ч, тогда скорость против течения равна (x-1) км/ч, а по течению — (x+1) км/ч. Время, затраченное против течения, равно 6/(x-1) ч, а по течению — 6/(x+1) ч. На весь путь байдарка затратила 6/(x-1) + 6/(x+1) ч, что по условию составляет 4ч30мин.
4 ч 30 мин = 4 ч+ 30/60ч = 4,5 ч.
Составим и решим уравнение:
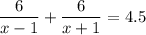
Для простоты умножим обе части уравнения на 2(x-1)(x+1)≠0
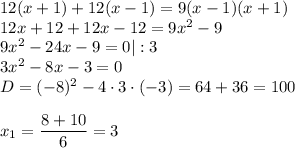
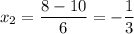 - не удовлетворяет условию
- не удовлетворяет условию
Собственная скорость байдарки составляет 3 км/ч.
Хв = -1, Ув = 1/4.
Подставляем в уравнение параболы и находим а:
1/4=a(-1)^2
а = 1/4.
Таким образом уравнение параболы:
y=1/4 x^2
Подставляем сюда y=9
9 = 1/4 x^2
x^2 = 36
х1 = 6, х2 = -6
Прямая y=9 пересекает параболу y=1/4 x^2 в двух точках А(6; 9) и С (-6; 9)