решить :
1)Разложите многочлен на множители: 4c²b + 3b² - 3ba - 4c²a
2)решите уравнение: 7z²+28z−(z+4)=0
3)Разложите многочлен на множители: c(a+b)+2a+2b
4)Разложите многочлен на множители: az⁴−ar+dr−dz⁴
5)Разложите многочлен на множители: 8a⁴ + 10a³ — 4a — 5
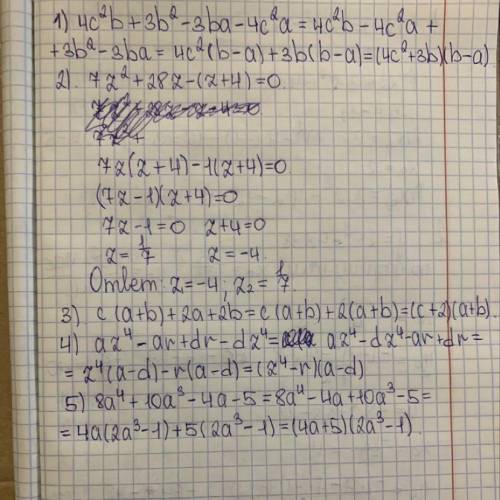
Решение в приложении
Объяснение: