 и
и  . Чтобы найти координату
. Чтобы найти координату  точек пересечения приравняем две функции (они пересекаются, значит приравниваем). Получаем:
точек пересечения приравняем две функции (они пересекаются, значит приравниваем). Получаем:
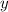 можем найти подставив
можем найти подставив  в выражение первой функции
в выражение первой функции  , а можно сделать проще. Так как пересечение будет с прямой
, а можно сделать проще. Так как пересечение будет с прямой  , то и точки пересечения будут иметь координату
, то и точки пересечения будут иметь координату  . Итак, получилось две точки пересечения с координатами:
. Итак, получилось две точки пересечения с координатами: 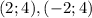 .
.![[0;1]](/tpl/images/0561/5883/90495.png) (этот отрезок по оси
(этот отрезок по оси  ), найдем значения
), найдем значения 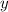 на концах этого отрезка:
на концах этого отрезка: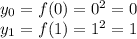
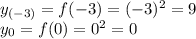

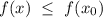

cos2y/2+cos2x/2
Объяснение:
1/2*(cos2y+cos2x)