а) Для определения вершины используем два уравнения. Для координаты по оси 
используем:
.
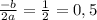Для координаты по оси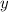 
используем:
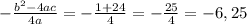
Координата вершины параболы: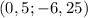 
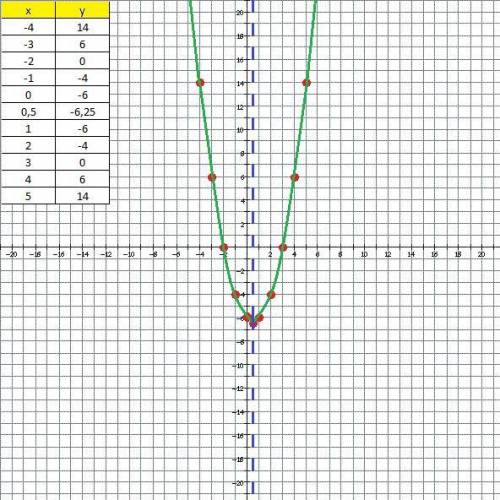
б) График находится во всех четырёх четвертях, но преимущественно, конечно, в I и II четвертях.
в) Ось симметрии проходит через вершину параболы и параллельно оси ординат. На графике отображается синим цветом пунктирная линия. Ось симметрии проходит при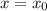 
.
г) Пересечение с осью ординат: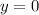 
при 
и при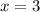 
Пересечение с осью абсцисс: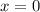 
при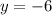 
д) Во вложении график функции.
а) х= 3
3²-4·3+3=0
9-12+3=0
0=0 - верное равенство, значит, число 3 является корнем уравнения х²-4х+3=0. Доказано.
б) х= - 7
2·(-7)²+(-7)-3=0
98-7-3=0
88≠0 - неверное равенство, значит, число -7 не является корнем уравнения 2х² +х-3=0.
в) х= -5
2·(-5)² - 3·(-5) - 65 =0
50+15-65 = 0
0 = 0 - верное равенство, значит, число -5 является корнем уравнения 2х² -3х-65=0.
г) х=6
6²-2·6+6=0
36-12+6 = 0
30≠0 - неверное равенство, значит, число 6 не является корнем уравнения х²-2х+6=0.