А1. У выражение -4m + 9n - 7m - 2n.
1) -3m + 11n
2) -3m + 7n
3) 11m + 7n
4) -11m + 7n
A2. Решите уравнение 5у + 1,5 = 2у - 7,5.
1) 6,375
2) 3
3) -3
4) 4
A3. У выражение с7 : c4 ∙ c.
1) c5
2) c6
3) c4
4) c12
A4. Выполните умножение и приведите подобные слагаемые (3a - b)(2b - 4a).
1) -12a2 – 10ab – 2b2
2) -12a2 + 10ab – 2b2
3) 6ab – 2b2
5) 6ab – 4b
A5. Преобразуйте в многочлен (4х – 5у)2.
1) 16х2 – 20ху + 25у2
2) 16х2 - 40ху + 25у2
3) 4х2 – 25у2
4) 16х2 – 25у2
A6. Один из смежных углов равен 20°. Найдите другой угол.
1) 700
2) 200
3) 1600
4) 1000
В задании В4 выполните построение с циркуля и линейки.
В4. Начертите три отрезка: 7см, 5см и 4см.
Постройте треугольник со сторонами, равными данным отрезкам.
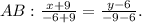
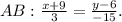
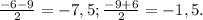
Используем распределительный закон ac + bc = c(a + b)Например - 12 y ^3 – 20 y ^2 = 4 y ^2 · 3 y – 4 y ^2 · 5 = 4 y ^2 (3 y – 5).
2)Использовать формулу сокращенного умножения.
x ^4 – 1 = ( x ^2 )^ 2 – 1 ^2 = ( x^ 2 – 1)( x^ 2 + 1) = ( x ^2 – 1 ^2 )( x ^2 + 1) = ( x + 1)( x – 1)( x 2 + 1).
группировки
x^3 – 3 x 2 y – 4 xy + 12 y ^2 = ( x ^3 – 3 x 2 y ) – (4 xy – 12 y ^2 ).
В первой группе мы вынесли за скобку общий множитель x^2, а во второй − 4y . В результате получаем:
( x ^3 – 3 x 2 y ) – (4 xy – 12 y ^2 ) = x 62 ( x – 3 y ) – 4 y ( x – 3 y ).
Теперь общий множитель ( x – 3 y ) можем вынести за скобки:
x ^2 ( x – 3 y ) – 4 y ( x – 3 y ) = ( x – 3 y )( x^2 – 4 y ).