Предположим, что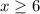 
является корнем уравнения. Тогда последний корень неотрицателен. Стало быть, левая часть не меньше ![\sqrt[3]{(6+3)^2} =3^{4/3}3](/tpl/images/1476/9468/2e007.png)
, противоречие.
Пусть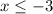 
является корнем уравнения. Получаем аналогичную ситуацию.
Значит, искомый корень лежит в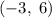 
(*).
Пусть ![\sqrt[3]{(x+3)^2}=a, \; \sqrt[3]{(6-x)^2} = b](/tpl/images/1476/9468/c8f10.png)
. Тогда уравнение можно переписать в виде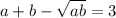 
. Домножим обе части на 
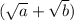, получим: 
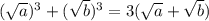. Левая часть уравнения равна 
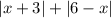. С учетом (*) можно записать 
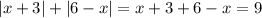. Наконец, 
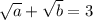. Исходное уравнение: 
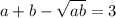. Возводя в квадрат первое уравнение и складывая со вторым, умноженным на 2, получаем 
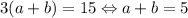. Если теперь возведенное в квадрат первое уравнение вычесть из второго, получим 
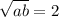. Из этой системы следует два решения: 
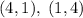. Вернемся к исходному уравнению: 
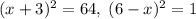, откуда 
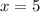. Второй случай: 
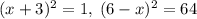, откуда 
.
|x²- x| +|2x-3| < x ;
|x(x-1)| +|2x-3| < x * * * ясно x >0 * * *
- - + - + +
0 1 1,5
Совокупность систем
a)
{0< x < 1 ; {0 < x < 1; { 0< x < 1 ;
{-x² +x -2x +3 < x . { x² +2x - 3 > 0 . { x ∈( -∞; -3) ∪ ( 1;∞).
x ∈ ∅ .
б)
{1≤ x < 1,5 ; { 1≤ x < 1,5 ; {1≤ x < 1,5 ;
{x² - x -2x +3 < x . { x² - 4x + 3 < 0 . { x ∈( 1 ; 3).
x ∈ ( 1;1,5) .
в)
{x ≥ 1,5 ; { x ≥ 1,5 ; { x ≥ 1,5 ;
{x² - x +2x -3 < x . { x² - 3 < 0 . { x ∈(-√3; √3).
x ∈ [1,5 ; √3) .
* * * x ∈ ( 1;1,5) ∪ [1,5 ; √3) = ( 1 ; √3) . * * *
ответ : x ∈ ( 1 ; √3) .
арифметику можно проверить