Дробь 
является неправильной рациональной дробью, так как степени многочленов в числителе и в знаменателе одинаковые и равны 1. Значит можно выделить целую и дробную часть неправильной дроби. Так как в знаменателе стоит многочлен 1 степени (линейная ф-ция) х+1, то и в числителе выделим х+1. Для этого надо вынести за скобки коэффициент (-5), который стоит перед х, и записать в скобках (х+1). Так как -5(х+1)=-5х-5, то , чтобы выражение не изменилось, надо добавить (+5), получим:
.
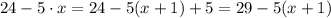Если в дальнейшем надо записать целую и дробную части неправильной рац. дроби, то
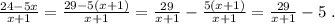
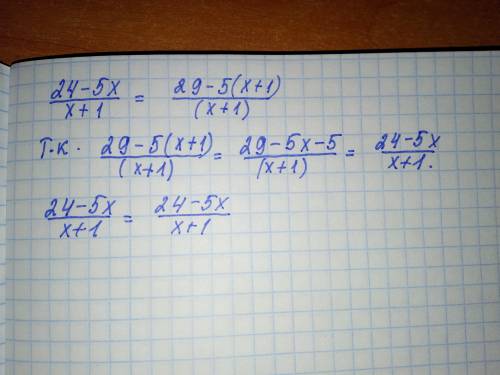
Скорость теплохода против течения реки: v₁ = v - v₀ = v - 6,5 (км/ч)
Скорость теплохода по течению реки: v₂ = v + v₀ = v + 6,5 (км/ч)
Время движения теплохода против течения: t₁ = S₁/(v - v₀) = 4/(v - 6,5) (ч)
Время движения теплохода по течению: t₂ = S₂/(v + v₀) = 33/(v + 6,5) (ч)
По условию, t = t₁ + t₂ = 1 (ч). Тогда:
4/(v - 6,5) + 33/(v + 6,5) = 1
4(v + 6,5) + 33(v - 6,5) = v² - 6,5²
4v + 26 + 33v - 214,5 - v² + 42,25 = 0
v² - 37v + 146,25 = 0
D = 1369 - 585 = 784 = 28²
v₁ = (-b+√D)/2a = (37+28)/2 = 32,5 (км/ч)
v₂ = (-b -√D)/2a = (37 - 28)/2 = 4,5 (км/ч) - не удовлетворяет условию, так как скорость теплохода не может быть меньше скорости течения.
ответ: 32,5 км/ч
Пересечение с осью ординат (0,2)
Объяснение: