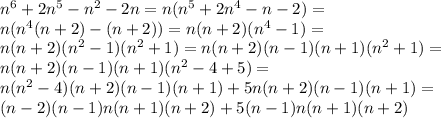
Мы получили два слогаемых рассмотрим первое: это произведение пяти последовательных чисел! значит одно из этих чисел должно делится на: 1 ,2, 3, 4 и 5.А число которое делится на эти числа - делится и на их произведение! Получим:
1*2*3*4*5=120 - мы получили что первое слогаемое делится на 120.
Рассмотрим второе слогаемое:произв. 4 последовательных чисел и при том -делится на 5. Получим: 1*2*3*4*5=120 - почти также как и первое слогаемое.
Мы получили сумму двух чисел ,каждое из которых делится на 120, значит и вся сумма делится на 120.
4 x2 + 4 x - 3 = 0
4 x2 + 4 x -3= 0
4 x2 +4 x -3= 0
Дискриминант: D = b2 - 4a*c = 42- 4*4*-3 = 64
Если D>0 то уравнение имеет 2 вещественных корня:
x1 =
(-b+√D)
=
(-4+√ 64)
=0.5
2a
2*4
x2 =
(-b-√D)
=
(-4-√ 64)
=-1.5
2a
2*4
5 x2 - 26 x + 5 = 0
5 x2 -26 x + 5= 0
5 x2 -26 x + 5= 0
Дискриминант: D = b2 - 4a*c = -262- 4*5*5 = 576
Если D>0 то уравнение имеет 2 вещественных корня:
x1 =
(-b+√D)
=
(26+√ 576)
=5
2a
2*5
x2 =
(-b-√D)
=
(26-√ 576)
=0.2
2a
2*5
x2 + 10 x + 24 = 0
x2 + 10 x + 24= 0
x2 +10 x + 24= 0
Дискриминант: D = b2 - 4a*c = 102- 4*1*24 = 4
Если D>0 то уравнение имеет 2 вещественных корня:
x1 =
(-b+√D)
=
(-10+√ 4)
=-4
2a
2*1
x2 =
(-b-√D)
=
(-10-√ 4)
=-6
2a
2*1
x2 - 50 x + 49 = 0
x2 -50 x + 49= 0
x2 -50 x + 49= 0
Дискриминант: D = b2 - 4a*c = -502- 4*1*49 = 2304
Если D>0 то уравнение имеет 2 вещественных корня:
x1 =
(-b+√D)
=
(50+√ 2304)
=49
2a
2*1
x2 =
(-b-√D)
=
(50-√ 2304)
=1
2a
2*1
xy=8x2+y2=20
Перенесем все в левую часть.
xy-8=0x2+y2-20=0
Произведем замену переменных.
u=x+y;v=xy
В результате замены переменных получаем вс систему уравнений.
v-8=0u2-2v-20=0
Из уравнения 1 выразим переменную v .
v=8u2-2v-20=0
Подставим вместо переменной v найденное выражение.
v=8u2-2·8-20=0
v=8u2-36=0
1 .
v=8u=-6
v=8u=6
Следующая система эквивалентна предыдущей.
xy=8x+y=-6xy=8x+y=6
xy=8x+y=-6
Из уравнения 2 выразим переменную x .
xy=8x=-6-y
xy=8x=-6-y
Преобразуем уравнение.
x=-6-y
x=-y-6
Подставим вместо переменной x найденное выражение.
-y-6y=8x=-y-6
Решаем вс уравнение.
-y-6y=8
Перенесем все в левую часть.
-y-6y-8=0
Изменим знаки выражений на противоположные.
-y+6y-8=0
Раскрываем скобки.
-y2+6y-8=0
Раскрываем скобки.
-y2-6y-8=0
Изменим знаки выражений на противоположные.
y2+6y+8=0
Находим дискриминант.
D=b2-4ac=62-4·1·8=4
Дискриминант положителен, значит уравнение имеет два корня.
Воспользуемся формулой корней квадратного уравнения.
y1,2=-b±D2a
y1=-6-22·1=-4 ;y2=-6+22·1=-2
ответ уравнения: y=-4;y=-2 .
y=-4x=-y-6
y=-4x=--4-6
y=-4x=-2
y=-2x=-y-6
y=-2x=--2-6
y=-2x=-4
xy=8x+y=6
Из уравнения 2 выразим переменную x .
xy=8x=6-y
Преобразуем уравнение.
x=6-y
x=-y+6
Подставим вместо переменной x найденное выражение.
-y+6y=8x=-y+6
Решаем вс уравнение.
-y+6y=8
Перенесем все в левую часть.
-y+6y-8=0
Изменим знаки выражений на противоположные.
-y-6y-8=0
Раскрываем скобки.
-y2-6y-8=0
Раскрываем скобки.
-y2+6y-8=0
Изменим знаки выражений на противоположные.
y2-6y+8=0
Находим дискриминант.
D=b2-4ac=-62-4·1·8=4
Дискриминант положителен, значит уравнение имеет два корня.
Воспользуемся формулой корней квадратного уравнения.
y1,2=-b±D2a
y1=6-22·1=2 ;y2=6+22·1=4
ответ уравнения: y=2;y=4 .
y=2x=-y+6
y=2x=-2+6
y=2x=4
y=4x=-y+6
y=4x=-4+6
y=4x=2
Окончательный ответ: (-2;-4), (-4;-2), (4;2), (2;4)
Объяснение: