(2 + x) (14 − x) = (2x − 8) (1 + 7x)
Чтобы умножить 2+x на 14−x, используйте свойство дистрибутивности и приведение подобных.
28 + 12x − x² = (2x − 8) (1 + 7x)
Чтобы умножить 2x−8 на 1+7x, используйте свойство дистрибутивности и приведение подобных.
28 + 12x − x² = −54x + 14x² − 8
Прибавьте 54x к обеим частям.
28 + 12x − x² + 54x = 14x² − 8
Объедините 12x и 54x, чтобы получить 66x.
28 + 66x − x² = 14x² − 8
Вычтите 14x² из обеих частей уравнения.
28 + 66x − x² − 14x² = −8
Объедините −x² и −14x² , чтобы получить −15x².
28 + 66x − 15x² = −8
Прибавьте 8 к обеим частям.
28 + 66x − 15x² + 8 = 0
Чтобы вычислить 36, сложите 28 и 8.
36 + 66x − 15x² = 0
Все уравнения вида ax² + bx + c = 0 можно решить с формулы корней квадратного уравнения 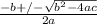
Эта формула дает два решения: одно, когда для ± используется сложение, а второе — когда вычитание.
−15x + 66x + 36 = 0
Данное уравнение имеет стандартный вид ax² +bx+c=0. Подставьте −15 вместо a, 66 вместо b и 36 вместо c в формуле корней квадратного уравнения 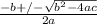
x₁ = 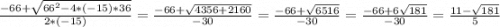
x₂ = 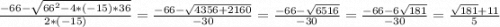
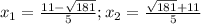
Решение системы уравнений у= -4
k= -11
Объяснение:
Решить систему уравнений методом подстановки.
5−5(0,2y−2k)=3(3k+2)+2y
4(k−5y)−(2k+y)=10−2(2k+y)
5-у+10k=9k+6+2y
4k-20y-2k-y=10-4k-2y
10k-9k-y-2y=6-5
2k+4k-21y+2y=10
k-3y=1
6k-19y=10
Выразим k через у в первом уравнении, подставим выражение во второе уравнение и вычислим у:
k=3y+1
6(3y+1)-19у=10
18у+6-19у=10
-у=10-6
-у=4
у= -4
k=3y+1
k=3*(-4)+1
k= -11
Решение системы уравнений у= -4
k= -11