Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру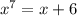 
уравнение в действительных корнях.
Рассмотрим функцию 
. Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию 
. Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение 
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
1) Он решил правильно. Возмем одного ученика. И допустим ево будет звать Миша. Например у Миши будет друг Андрей. Миша и Андрей возьмуться за руки и в это цепочку добавим еще 10 человек.И так возьмется каждый человек за руку со своими 11ю друзьями. Тогда количество рук можно вичислить если умножить 35 человек на 11 последующих друзей и это будет 385 рук. Но как известно руки у нас две а не три или пять. Значит число должно получиться четное.опустим если бы он сказал что в классе 35 человек и каждый дружит ровно с 12 одноклассниками то получилось бы 420 и это была бы правда т.к 420 четное число.
3) то это 1, да это это 1 да половина того одна вторая
"То" да "это", да половина "того" да "этого": 1+1+1/2+1/2=3
Три четверти "того" да "этого": 3/4+3/4=6/4=3/2=1,5