Рівняння дотичної до графіка функції y=2sin4x має вигляд y=-8x+1. Знайти абсцису точки дотику.

👇

Открыть все ответы

Ответ:

Xzxzxzxzxzzxzxz

13.04.2021

Уравнение четвёртой степени имеет вид:
$\alpha _0x^4+ \alpha _1x^3+ \alpha _2x^2+ \alpha _3x+ \alpha _4=0$
Разделим обе части на коэффициент $\alpha _0$ , получаем
$x^4+ \alpha x^3+ bx^2+cx+d=0$
где a, b, c, d – произвольные вещественные числа.

Уравнения вида приводится уравнение четвёртой степени, у которых отсувствует третьей степени., поэтому нужно сделать замену переменных, тоесть
$x=i- \frac{ \alpha }{4}$ , где $\alpha$ - коэффициент перед х^3 и 4 - произвольные вещественные числа

В нашем случае такое уравнение: x^4+6x^3-21x^2+78x-16=0

Заменим $x=i- \frac{6}{4} =i-1.5$ , получаем
$(i-1.5)^4+6(i-1.5)^3-21(i-1.5)^2+78(i-1.5)-16=0\\ i^4-6i^3+13.5i^2-13.5i+5.0625+6i^3-27i^2+40.5i-20.25-21i^2+\\+63i-47.25+78i-117-16=0\\ i^4-34.5i^2+168i-195.4375=0$

Получаем кубическое уравнение: $2s^3-ps^2-2rs+rp- \frac{q^2}{4}=0$
В нашем случае: $p=-34.5;\,\,\,\,q=168;\,\,\,\,r=-195.4375$
Подставляем и получаем уравнение
$2s^3+34.5s^2+2\cdot195.4375s+34.5\cdot195.4375- \frac{168^2}{4}=0\\ 64s^3-1104s^2+12508s-10029=0$
Разложим одночлены в сумму нескольких
64s^3-48s^2+1152s^2-864s+13372s-10029=0

Выносим общий множитель
$16s^2(4s-3)+288s(4s-3)+3343(4s-3)=0\\ (4s-3)(16s^2+288s+3343)=0\\ s=0.75$
Уравнение 16s²+288s+3343=0 решений не имеет, так как D<0

Таким образом для решения уравнения остается квадратное уравнение
$i^2+i \sqrt{2s-p} - \frac{q}{2\sqrt{2s-p}}+s=0$
Заменяем
$i^2+i\sqrt{2\cdot0.75+34.5}- \frac{168}{\sqrt{2\cdot0.75+34.5}} +0.75=0\\ 4i^2+24i-53=0\\ D=b^2-4ac=576+848=1424\\ i= \dfrac{-6\pm \sqrt{89} }{2}$

Возвращаемся к замене
$x=i-1.5=\dfrac{-6\pm \sqrt{89} }{2}- \dfrac{3}{2} =\dfrac{-9\pm \sqrt{89} }{2}$

Окончательный ответ: $\dfrac{-9\pm \sqrt{89} }{2}.$

4,6(12 оценок)

Ответ:

tatsawi

13.04.2021

Здесь заметим, что первый из углов - это 2π или π/2. Значит, воспользуемся формулами приведения:

ctg(2п+a)*sin(п\2+a) / (cos(п-a)*tg(3п\2-a) = ctg a * cos a / -cos a * ctg a = cos a / -cos a = -1

Cначала преобразуем числитель отдельно. Для его преобразований воспользуемся формулами двойного аргумента.

16sin12º*cos12º*cos24º = 8 * 2sin12º*cos12º*cos24º = 8sin 24°cos 24° = 4 * 2sin 24°cos 24° = 4sin 48°

Получим,

4sin 48° / cos 42° = 4sin(90° - 42°) / cos 42° = 4cos 42° / cos 42° = 4

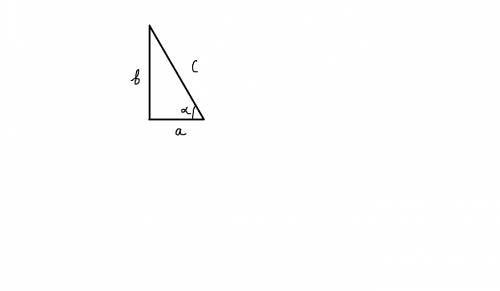
Здесь вся сложность заключается в том, чтобы найти точное значение выражения ctg(arccos 1/4). Поэтому для его нахождения воспользуемся методом прямоугольного треугольника(рисунок сейчас приложу). Рассмотрим прямоугольный треугольник.

Пусть arccos 1/4 = α, тогда по определению арккосинуса cosα = 1/4

По сути, как несложно догадаться, нам нужно найти ctg α, зная его косинус.

cos α = a/c

a/c = 1/4, отсюда a = 1, c = 4

ctg α = a/b, не хватает только лишь b. Найдём её по теореме Пифагора,

b² = c² - a²

b² = 16 - 1 = 15

b = √15

Тогда, ctg α = a/b = 1/√15 = √15/15

Но α = arccos 1/4. Значит, ctg(arccos 1/4) = √15/15

Теперь осталось только верно посчитать:

2⁻² = 1/4