Решение в приложении
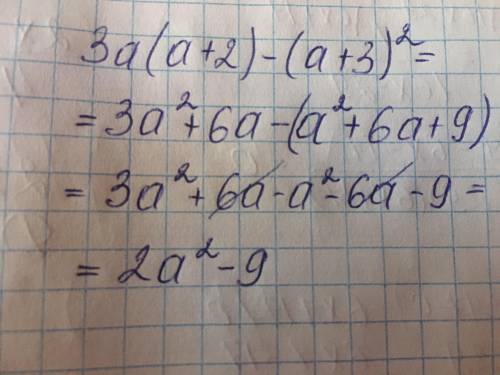
В решении.
Объяснение:
Яка точка належить графіку рівняння x+y=9 (-6;-3); (6;3); (7;3); (1;9).
Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение. Если левая часть равна правой, то принадлежит, и наоборот.
а)x+y=9 (-6;-3);
-6-3= -9
-9≠9, не принадлежит.
б)x+y=9 (6;3);
6+3=9
9=9, принадлежит.
в)x+y=9 (7;3);
7+3=10
10≠9, не принадлежит.
г)x+y=9 (1;9)
1+9=10
10≠9, не принадлежит.
б.
Оскільки периметр обчислюється за формулою P = 2 • (a + b), де а - довжина, b - ширина, тоді сума довжини і ширини рівна половині периметра,
тобто а + b = Р:2
За умовою задачі довжина b=a+40, тому а+а+40=P:2
680 : 2 = 340 (м) – сума довжини та ширини ділянки.
340 – 40 = 300 (м) – подвійна ширина ділянки.
300 : 2 = 150 (м) – ширина ділянки.
150 + 40 = 190 (м) – довжина ділянки.
б.
Нехай х (м) – ширина ділянки , тоді х + 40 (м) – довжина ділянки, складемо рівняння:
Периметр обчислюється за формулою P = 2 • (a + b), де а - довжина, b - ширина.
2 • ( х + х + 40)= 680
Щоб знайти невідомий множник, треба добуток поділити на відомий множник.
(х + х + 40) = 680 : 2
2х + 40 = 340
Щоб знайти невідомий доданок, треба від суми відняти відомий доданок.
2х = 340 – 40
2х = 300
х = 300 : 2
х = 150
150 (м) – ширина ділянки, тоді
150 + 40 = 190 (м) – довжина ділянки.
Відповідь: 190 метрів.
Объяснение:
3a(a+2)-(a+3)²= 3a²+6a-a²-6a-9= 2a²-9