x² + (m - 1)x + m² - 1,5 = 0
По теореме Виета :
x₁ + x₂ = - (m - 1)
x₁ * x₂ = m² - 1,5
x₁² + x₂² = (x₁ + x₂)² - 2x₁ * x₂ = (- (m - 1))² - 2 * (m² - 1,5) = m² - 2m + 1 - 2m² + 3 = - m² - 2m + 4
Найдём производную полученного выражения :
(- m² - 2m + 4)'= -2m - 2
Приравняем к нулю и найдём нули производной :
- 2m - 2 = 0
m + 1 = 0
m = - 1
Отметим полученное число на числовой прямой и найдём знаки производной на промежутках, на которые разбивается числовая прямая :
+ -
- 1
↑ max ↓
ответ : при m = - 1 сумма корней уравнения наибольшая
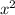-3|x|+1=1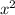-3|x|=0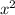-3|x|+1=-1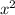-3|x|=-2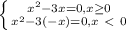
a[1]=0
a[n]=3a[n-1]+2 - рекурентная формула
2=3*0+2
8=3*2+2
26=3*8+2
80=3*26+2
a[1]=0=3^(1-1)-1
a[2]=2=3^(2-1)-1
a[3]=8=3^(3-1)-1
a[4]=26=3^(4-1)-1
a[5]=0=3^(5-1)-1
a[n]=3^(n-1) -1 - нерекурентная формула