1. Найти точку минимума функции: 
Найдём производную: 
Приравняем производную к нулю:

 | :3
| :3
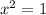
 или
или 
Рисуем координатную ось и проверяем знаки, получаем: + - +
Точка минимума: с - на +
ответ: 1
2. Найдите наименьшее значение функции на отрезке [0;3]
Из ранее вычисленного проверяем точки, которые подходят в заданный отрезок [0;3]. Из этого следует, что точка -1 не подходит.
Считаем в точке.
f(0)= 0
f(3)= 
f(1)= 
ответ: -2
3. Найдите значение функции в точке максимума: 
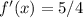
Одна точка и она же максимум.
ответ: 1,25
x₁=1
2x⁴+7x³-3x²-5x-1 I_x-1_
2x⁴-2x³ I 2x³+9x²+6x+1
9x³-3x²
9x³-9x²
6x²-5x
6x²-6x
x-1
x-1
0
2x³+9x²+6x+1=0 I÷2
x³+4,5x²+3x+0,5=0
x₂=-0,5
x³+4,5x+3x+0,5 I_x+0,5_
x³+0,5x² I x²+4x+1
4x²+3x
4x²+2x
x+0,5
x+0,5
0
x²+4x+1=0 D=12 ⇒ √D-√12, то есть корни этого уравнения будут иррациональными.
ответ: х₁=1 х₂=-0,5.