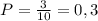
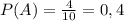
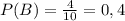
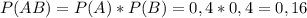
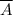Алгебра: Зведіть подібні доданки 9у+2-11у Заранее

Зведіть подібні доданки 9у+2-11у Заранее

👇

Увидеть ответ

Ответ:

minat2

25.01.2022

1. Подобные:9у и 11у.

2. Подобные:2 и 17.

1. 9у-11у=-2у

2. 2-17=-15

-2у-15

Удачи!;)

4,4(62 оценок)

Открыть все ответы

Ответ:

ВикаЛук1

25.01.2022

1. В вазе лежат 11 фруктов: 7 яблок и 4 груши. Сначала из вазы извлекли 1 грушу, т.е. это нам известно (вероятность 1). В вазе осталось 10 фруктов: 7 яблок и 3 груши. Вероятность того, что в этот раз будет взята груша равна:
$P = \frac{3}{10} =0,3$

2. В коробке лежат 10 деталей: 6 нормальных и 4 более лёгких. Значит, вероятность вытянуть из коробки лёгкую деталь равна (пусть это будет событие А):
$P(A) = \frac{4}{10} = 0,4$
На 6 деталей из 10 случайно сделали напыление. Тогда вероятность вытянуть деталь без напыления (пусть это будет событие В) равна:
$P(B) = \frac{4}{10} = 0,4$
Т.к. события А и В независимы, то вероятность их совместного появления равна произведению вероятностей:
P(AB) = P(A)*P(B) = 0,4 * 0,4 = 0,16

3. В вазе 11 цветков: 5 гвоздик и 6 нарциссов. Надо найти вероятность того, что среди 3 случайно вынутых цветков будет по крайней мере 1 гводика (пусть это событие А). Заметим, что собтытие, когда среди трёх вытащенных цветов все нарциссы, является противоположным событию А. Обозначим его $\overline{A}$ и найдём его вероятность.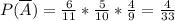
Вероятность, что первым вытянутым цветком будет нарцисс, равна 6/11. Вероятность, что и второй цветок окажется нарциссом, равна 5/10. И наконец, вероятность, что и третий цветок будет нарциссом, равна 4/9. Т.к. события незавичимы, то вероятности перемножаем:
$P(\overline{A}) = \frac{6}{11}* \frac{5}{10}* \frac{4}{9} = \frac{4}{33}$
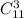Есть другой вариант вычисления данной вероятности. Надо вычислить, сколько всего есть вариантов вытащить 3 цветка из 11 (это число сочетаний по 3 из 11 - $C_{11} ^3$ ). И вычислить число вариантов выбора 3 нарциссов из 6 ( C_6^3

). А потом по классической формуле вероятности находится требуемая вероятность. Не всегда, но в данном случае такой путь боле громоздок.

Теперь остаётся найти нужную вероятность:
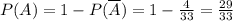
$P(A) = 1 -P(\overline{A}) = 1 - \frac{4}{33} = \frac{29}{33}$

4,7(73 оценок)

Ответ:

динька2

25.01.2022

h₂ = 16/3 см или h₂ = 3 см.

Объяснение:

Дано:

Параллелограмм ABCD

AB = CD = 9 см

BC = AD = 12 см

h₁ = 4 см - высота, соответствующая одной стороне

Найти: вторую высоту h₂, соответствующей второй стороне.

Решение.

Воспользуемся формулой площади параллелограмма: S = a·h, то есть площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

Возможны 2-случая.

1-случай (см. рисунок-1): S = AD·h₁ = 12·4 (см²) = 48 (см²).

Для нахождения вторую высоту h₂, соответствующей второй стороне опять воспользуемся формулой площади параллелограмма:

S = CD·h₂ = 48 (см²)

Отсюда:

9 см · h₂ = 48 (см²)

h₂ = 48 : 9 см = 16/3 см = 5 1/3 см.

ответ: h₂ = 16/3 см = 5 1/3 см.

2-случай (см. рисунок-2): S = CD·h₁ = 9·4 (см²) = 36 (см²).

S = AD·h₂ = 36 (см²)

Отсюда:

12 см · h₂ = 36 (см²)