Найдем, какую часть бассейна сможет наполнить каждая из труб за один час.
В условии задачи сказано, что первая труба может наполнить бассейн за 3 часа, а вторая труба наполняет весь бассейн за 2 часа, следовательно, за 1 час первая труба сможет наполнить 1/3 часть бассейна, а вторая труба сможет наполнить 1/2 часть бассейна.
Тогда, при совместной работе две трубы за 1 час смогут наполнить 1/2 + 1/3 = 3/6 + 2/6 = 5/6 частей бассейна, а весь бассейн наполнят за 6/5 ч , что в минутах составляет (6/5) * 60 = 6 * 60 / 5 = 6 * 12 = 72 мин.
ответ: за 72 минуты.
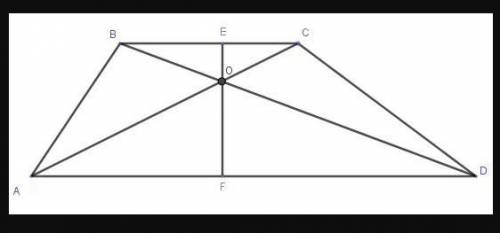
EO и OF - являются расстояниями от точки пересечения диагоналей до основания BC и AD, соответственно. ЕО - высота треугольника BOC и OF - высота треугольника AOD.
∠BCA = ∠CAD как накрест лежащие при BC || AD и секущей AC
∠BOC = ∠AOD как вертикальные
Следовательно, ΔBOC ~ ΔAOD (по двум углам).
Соответствующие высоты подобных треугольников относятся как соответствующие стороны, их коэффициент подобия есть отношение расстояний k = OF/OE =6/2=3
Пусть BC = x см, тогда AD = 3x см. Из условия BC + AD = 36
x + 3x = 36
4x = 36
x = 9 см.
Итак, основания трапеции 9 см и 3*9 = 27 см.
Объяснение:
Объяснение:
f'(x)= 6x²+6x-36
x²+x-6=0
D= 1+24= 25
x1= (-1-5)/2= -3
x2= (-1+5)/2= 2
f(-3)=81
f(2)= -44
x=2 точка минимума, x= -3 точка максимума