Пояснение:
Это квадратное уравнение можно решить сразу тремя : через теорему Виета и через Дискриминант (полный и краткий). Покажу все три.
(теорема Виета)
- можно применять, если первый (старший) коэффициент (а) равен единице (1), то есть квадратное уравнение имеет вид:
x² ± px ± q = 0.
x² + 8x + 15 = 0
p = 8; q = 15.
По т. Виета:
x₁ + x₂ = - 8,
x₁ × x₂ = 15.
x₁ = - 5,
x₂ = - 3.
<><><><><><><><><><><><><><><><>
IIа (Дискриминант)
- можно применять к любым полным квадратным уравнениям вида:
ax² ± bx ± c = 0.
x² + 8x + 15 = 0
a = 1; b = 8; c = 15.
D = b² - 4ac = 8² - 4 × 1 × 15 = 64 - 60 = 4 = 2².
D > 0 (значит, уравнение имеет два действ. корня)
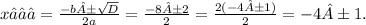
x₁ = - 4 - 1 = - 5,
x₂ = - 4 + 1 = - 3.
<><><><><><><><><><><><><><><><>
IIб ("краткий" Дискриминант)
- можно применять к любым полным квадратным уравнениям вида:
- можно применять к любым полным квадратным уравнениям вида:ax² ± bx ± c = 0,
где b - чётное число (то есть делится на 2 без остатка).
x² + 8x + 15 = 0
a = 1; b = 8; c = 15.
k = b ÷ 2 = 8 ÷ 2 = 4.
D₁ = k² - ac = 4² - 1 × 15 = 16 - 15 = 1.
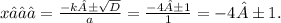
x₁ = - 4 - 1 = - 5,
x₂ = - 4 + 1 = - 3.
<><><><><><><><><><><><><><><><>
ответ: - 5; - 3.
Удачи Вам! :)
36; 35; 15;36
Объяснение:
1. Составим систему
х+у=51
х-у=21
х=21+у
21+у+у=51
2у=51-21
2у=30
у=30:2
у=15
х+15=51
х=51-15
х=36
2. В данном случае, в качестве неизвестного Х возьмем количество книг на первой полке, тогда на второй полке будет Х-10 книг. Так как общее количество книг равно 60, то теперь составим уравнение, которое будет иметь вид:
Х + (Х-10) = 60.
Решаем.
2 * Х = 60 + 10
2 * Х = 70
Х = 70 : 2
Х = 35
Таким образом получаем, что на первой полке 35 книг, соответственно на второй будет на 10 меньше и равняется 25.
ответ: на первой полке 35 книг.
3. Представим первое число как 5 частей, а второе как 12 частей.
12-5=7 это разность их частей, то есть 7 частей соответствует 21
21/7=3 это одна часть
5*3=15 это первое число
3*12=36 это второе число
ответ: 15;36